Adaptive Graph Learning from Spatial Information for Surgical Workflow Anticipation

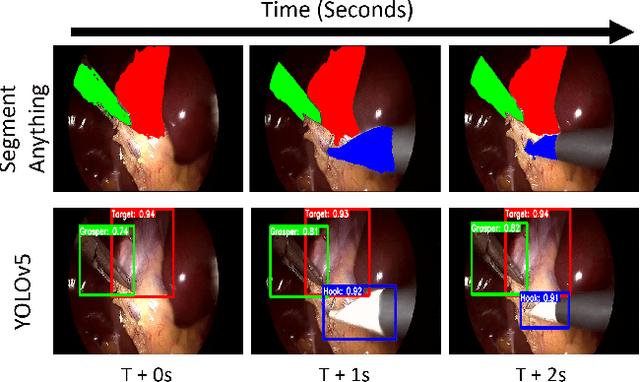
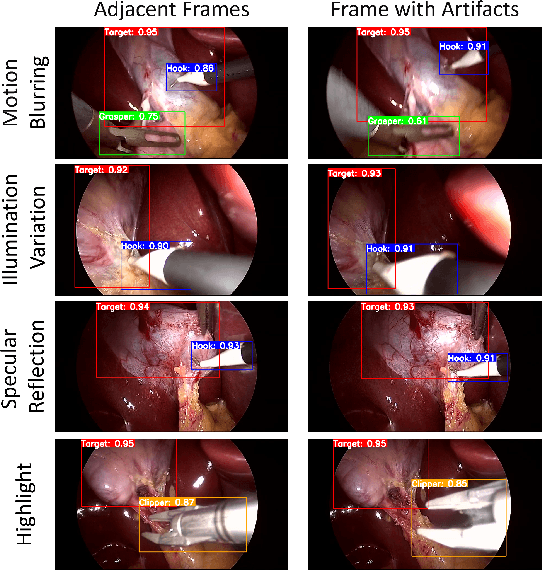
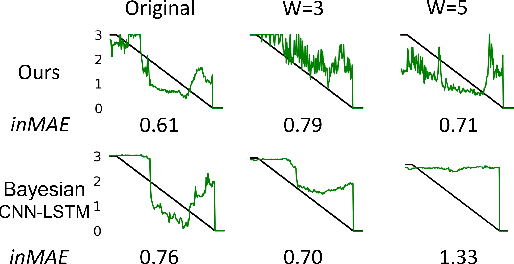
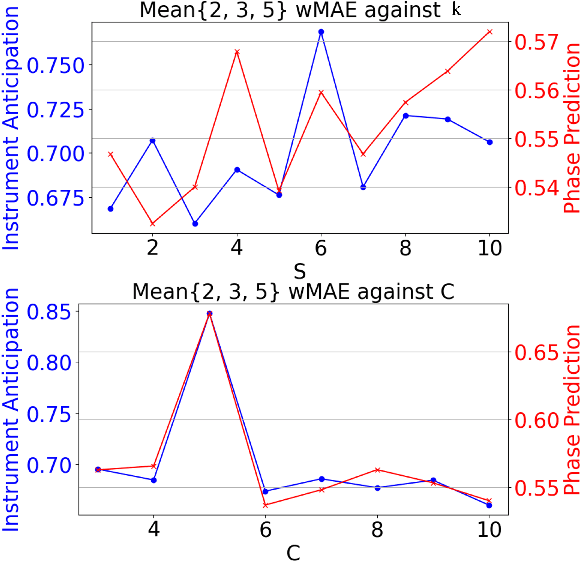
Surgical workflow anticipation is the task of predicting the timing of relevant surgical events from live video data, which is critical in Robotic-Assisted Surgery (RAS). Accurate predictions require the use of spatial information to model surgical interactions. However, current methods focus solely on surgical instruments, assume static interactions between instruments, and only anticipate surgical events within a fixed time horizon. To address these challenges, we propose an adaptive graph learning framework for surgical workflow anticipation based on a novel spatial representation, featuring three key innovations. First, we introduce a new representation of spatial information based on bounding boxes of surgical instruments and targets, including their detection confidence levels. These are trained on additional annotations we provide for two benchmark datasets. Second, we design an adaptive graph learning method to capture dynamic interactions. Third, we develop a multi-horizon objective that balances learning objectives for different time horizons, allowing for unconstrained predictions. Evaluations on two benchmarks reveal superior performance in short-to-mid-term anticipation, with an error reduction of approximately 3% for surgical phase anticipation and 9% for remaining surgical duration anticipation. These performance improvements demonstrate the effectiveness of our method and highlight its potential for enhancing preparation and coordination within the RAS team. This can improve surgical safety and the efficiency of operating room usage.

Planning Transformer: Long-Horizon Offline Reinforcement Learning with Planning Tokens

Supervised learning approaches to offline reinforcement learning, particularly those utilizing the Decision Transformer, have shown effectiveness in continuous environments and for sparse rewards. However, they often struggle with long-horizon tasks due to the high compounding error of auto-regressive models. To overcome this limitation, we go beyond next-token prediction and introduce Planning Tokens, which contain high-level, long time-scale information about the agent's future. Predicting dual time-scale tokens at regular intervals enables our model to use these long-horizon Planning Tokens as a form of implicit planning to guide its low-level policy and reduce compounding error. This architectural modification significantly enhances performance on long-horizon tasks, establishing a new state-of-the-art in complex D4RL environments. Additionally, we demonstrate that Planning Tokens improve the interpretability of the model's policy through the interpretable plan visualisations and attention map.

Recursive Bayesian Networks: Generalising and Unifying Probabilistic Context-Free Grammars and Dynamic Bayesian Networks

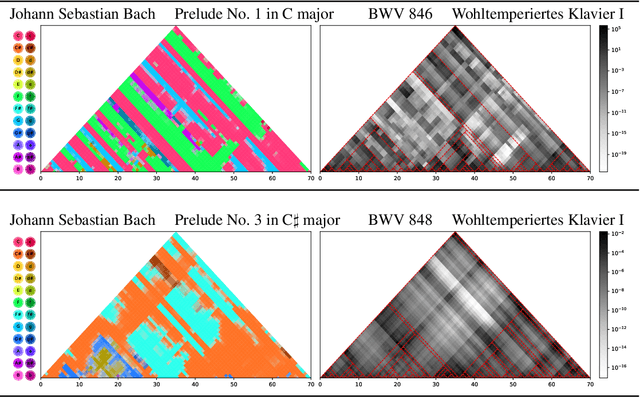
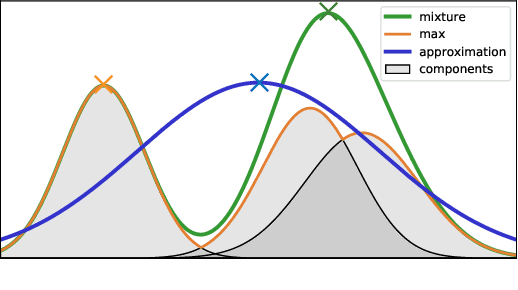
Probabilistic context-free grammars (PCFGs) and dynamic Bayesian networks (DBNs) are widely used sequence models with complementary strengths and limitations. While PCFGs allow for nested hierarchical dependencies (tree structures), their latent variables (non-terminal symbols) have to be discrete. In contrast, DBNs allow for continuous latent variables, but the dependencies are strictly sequential (chain structure). Therefore, neither can be applied if the latent variables are assumed to be continuous and also to have a nested hierarchical dependency structure. In this paper, we present Recursive Bayesian Networks (RBNs), which generalise and unify PCFGs and DBNs, combining their strengths and containing both as special cases. RBNs define a joint distribution over tree-structured Bayesian networks with discrete or continuous latent variables. The main challenge lies in performing joint inference over the exponential number of possible structures and the continuous variables. We provide two solutions: 1) For arbitrary RBNs, we generalise inside and outside probabilities from PCFGs to the mixed discrete-continuous case, which allows for maximum posterior estimates of the continuous latent variables via gradient descent, while marginalising over network structures. 2) For Gaussian RBNs, we additionally derive an analytic approximation, allowing for robust parameter optimisation and Bayesian inference. The capacity and diverse applications of RBNs are illustrated on two examples: In a quantitative evaluation on synthetic data, we demonstrate and discuss the advantage of RBNs for segmentation and tree induction from noisy sequences, compared to change point detection and hierarchical clustering. In an application to musical data, we approach the unsolved problem of hierarchical music analysis from the raw note level and compare our results to expert annotations.

Towards Moral Autonomous Systems

Both the ethics of autonomous systems and the problems of their technical implementation have by now been studied in some detail. Less attention has been given to the areas in which these two separate concerns meet. This paper, written by both philosophers and engineers of autonomous systems, addresses a number of issues in machine ethics that are located at precisely the intersection between ethics and engineering. We first discuss the main challenges which, in our view, machine ethics posses to moral philosophy. We them consider different approaches towards the conceptual design of autonomous systems and their implications on the ethics implementation in such systems. Then we examine problematic areas regarding the specification and verification of ethical behavior in autonomous systems, particularly with a view towards the requirements of future legislation. We discuss transparency and accountability issues that will be crucial for any future wide deployment of autonomous systems in society. Finally we consider the, often overlooked, possibility of intentional misuse of AI systems and the possible dangers arising out of deliberately unethical design, implementation, and use of autonomous robots.

The Advantage of Cross Entropy over Entropy in Iterative Information Gathering

Gathering the most information by picking the least amount of data is a common task in experimental design or when exploring an unknown environment in reinforcement learning and robotics. A widely used measure for quantifying the information contained in some distribution of interest is its entropy. Greedily minimizing the expected entropy is therefore a standard method for choosing samples in order to gain strong beliefs about the underlying random variables. We show that this approach is prone to temporally getting stuck in local optima corresponding to wrongly biased beliefs. We suggest instead maximizing the expected cross entropy between old and new belief, which aims at challenging refutable beliefs and thereby avoids these local optima. We show that both criteria are closely related and that their difference can be traced back to the asymmetry of the Kullback-Leibler divergence. In illustrative examples as well as simulated and real-world experiments we demonstrate the advantage of cross entropy over simple entropy for practical applications.