Hamiltonian Adaptive Importance Sampling

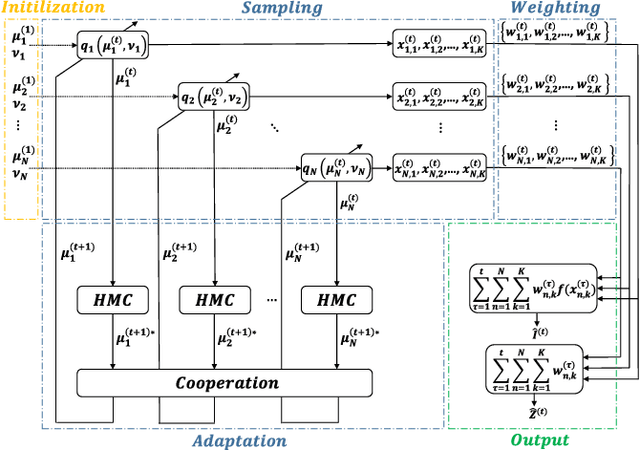
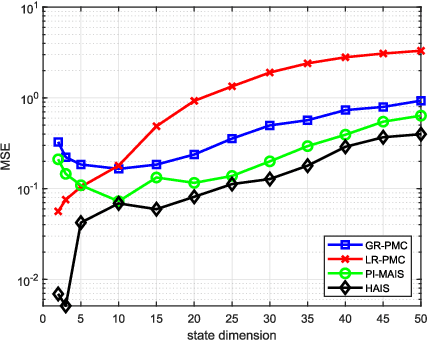
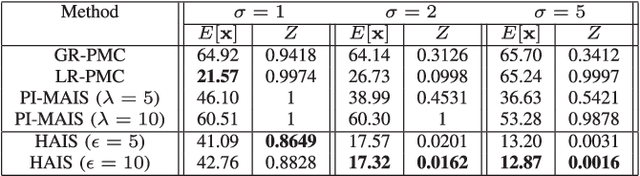
Importance sampling (IS) is a powerful Monte Carlo (MC) methodology for approximating integrals, for instance in the context of Bayesian inference. In IS, the samples are simulated from the so-called proposal distribution, and the choice of this proposal is key for achieving a high performance. In adaptive IS (AIS) methods, a set of proposals is iteratively improved. AIS is a relevant and timely methodology although many limitations remain yet to be overcome, e.g., the curse of dimensionality in high-dimensional and multi-modal problems. Moreover, the Hamiltonian Monte Carlo (HMC) algorithm has become increasingly popular in machine learning and statistics. HMC has several appealing features such as its exploratory behavior, especially in high-dimensional targets, when other methods suffer. In this paper, we introduce the novel Hamiltonian adaptive importance sampling (HAIS) method. HAIS implements a two-step adaptive process with parallel HMC chains that cooperate at each iteration. The proposed HAIS efficiently adapts a population of proposals, extracting the advantages of HMC. HAIS can be understood as a particular instance of the generic layered AIS family with an additional resampling step. HAIS achieves a significant performance improvement in high-dimensional problems w.r.t. state-of-the-art algorithms. We discuss the statistical properties of HAIS and show its high performance in two challenging examples.

Deep Learning Applications for Lung Cancer Diagnosis: A systematic review

Lung cancer has been one of the most prevalent disease in recent years. According to the research of this field, more than 200,000 cases are identified each year in the US. Uncontrolled multiplication and growth of the lung cells result in malignant tumour formation. Recently, deep learning algorithms, especially Convolutional Neural Networks (CNN), have become a superior way to automatically diagnose disease. The purpose of this article is to review different models that lead to different accuracy and sensitivity in the diagnosis of early-stage lung cancer and to help physicians and researchers in this field. The main purpose of this work is to identify the challenges that exist in lung cancer based on deep learning. The survey is systematically written that combines regular mapping and literature review to review 32 conference and journal articles in the field from 2016 to 2021. After analysing and reviewing the articles, the questions raised in the articles are being answered. This research is superior to other review articles in this field due to the complete review of relevant articles and systematic write up.

Vector Transport Free Riemannian LBFGS for Optimization on Symmetric Positive Definite Matrix Manifolds

This work concentrates on optimization on Riemannian manifolds. The Limited-memory Broyden-Fletcher-Goldfarb-Shanno (LBFGS) algorithm is a commonly used quasi-Newton method for numerical optimization in Euclidean spaces. Riemannian LBFGS (RLBFGS) is an extension of this method to Riemannian manifolds. RLBFGS involves computationally expensive vector transports as well as unfolding recursions using adjoint vector transports. In this article, we propose two mappings in the tangent space using the inverse second root and Cholesky decomposition. These mappings make both vector transport and adjoint vector transport identity and therefore isometric. Identity vector transport makes RLBFGS less computationally expensive and its isometry is also very useful in convergence analysis of RLBFGS. Moreover, under the proposed mappings, the Riemannian metric reduces to Euclidean inner product, which is much less computationally expensive. We focus on the Symmetric Positive Definite (SPD) manifolds which are beneficial in various fields such as data science and statistics. This work opens a research opportunity for extension of the proposed mappings to other well-known manifolds.

A Framework to Enhance Generalization of Deep Metric Learning methods using General Discriminative Feature Learning and Class Adversarial Neural Networks

Metric learning algorithms aim to learn a distance function that brings the semantically similar data items together and keeps dissimilar ones at a distance. The traditional Mahalanobis distance learning is equivalent to find a linear projection. In contrast, Deep Metric Learning (DML) methods are proposed that automatically extract features from data and learn a non-linear transformation from input space to a semantically embedding space. Recently, many DML methods are proposed focused to enhance the discrimination power of the learned metric by providing novel sampling strategies or loss functions. This approach is very helpful when both the training and test examples are coming from the same set of categories. However, it is less effective in many applications of DML such as image retrieval and person-reidentification. Here, the DML should learn general semantic concepts from observed classes and employ them to rank or identify objects from unseen categories. Neglecting the generalization ability of the learned representation and just emphasizing to learn a more discriminative embedding on the observed classes may lead to the overfitting problem. To address this limitation, we propose a framework to enhance the generalization power of existing DML methods in a Zero-Shot Learning (ZSL) setting by general yet discriminative representation learning and employing a class adversarial neural network. To learn a more general representation, we propose to employ feature maps of intermediate layers in a deep neural network and enhance their discrimination power through an attention mechanism. Besides, a class adversarial network is utilized to enforce the deep model to seek class invariant features for the DML task. We evaluate our work on widely used machine vision datasets in a ZSL setting.

Accurate and fast matrix factorization for low-rank learning

In this paper we tackle two important challenges related to the accurate partial singular value decomposition (SVD) and numerical rank estimation of a huge matrix to use in low-rank learning problems in a fast way. We use the concepts of Krylov subspaces such as the Golub-Kahan bidiagonalization process as well as Ritz vectors to achieve these goals. Our experiments identify various advantages of the proposed methods compared to traditional and randomized SVD (R-SVD) methods with respect to the accuracy of the singular values and corresponding singular vectors computed in a similar execution time. The proposed methods are appropriate for applications involving huge matrices where accuracy in all spectrum of the desired singular values, and also all of corresponding singular vectors is essential. We evaluate our method in the real application of Riemannian similarity learning (RSL) between two various image datasets of MNIST and USPS.

Neural Generalization of Multiple Kernel Learning

Multiple Kernel Learning is a conventional way to learn the kernel function in kernel-based methods. MKL algorithms enhance the performance of kernel methods. However, these methods have a lower complexity compared to deep learning models and are inferior to these models in terms of recognition accuracy. Deep learning models can learn complex functions by applying nonlinear transformations to data through several layers. In this paper, we show that a typical MKL algorithm can be interpreted as a one-layer neural network with linear activation functions. By this interpretation, we propose a Neural Generalization of Multiple Kernel Learning (NGMKL), which extends the conventional multiple kernel learning framework to a multi-layer neural network with nonlinear activation functions. Our experiments on several benchmarks show that the proposed method improves the complexity of MKL algorithms and leads to higher recognition accuracy.

Robust Metric Learning based on the Rescaled Hinge Loss

Distance/Similarity learning is a fundamental problem in machine learning. For example, kNN classifier or clustering methods are based on a distance/similarity measure. Metric learning algorithms enhance the efficiency of these methods by learning an optimal distance function from data. Most metric learning methods need training information in the form of pair or triplet sets. Nowadays, this training information often is obtained from the Internet via crowdsourcing methods. Therefore, this information may contain label noise or outliers leading to the poor performance of the learned metric. It is even possible that the learned metric functions perform worse than the general metrics such as Euclidean distance. To address this challenge, this paper presents a new robust metric learning method based on the Rescaled Hinge loss. This loss function is a general case of the popular Hinge loss and initially introduced in (Xu et al. 2017) to develop a new robust SVM algorithm. In this paper, we formulate the metric learning problem using the Rescaled Hinge loss function and then develop an efficient algorithm based on HQ (Half-Quadratic) to solve the problem. Experimental results on a variety of both real and synthetic datasets confirm that our new robust algorithm considerably outperforms state-of-the-art metric learning methods in the presence of label noise and outliers.

RELF: Robust Regression Extended with Ensemble Loss Function

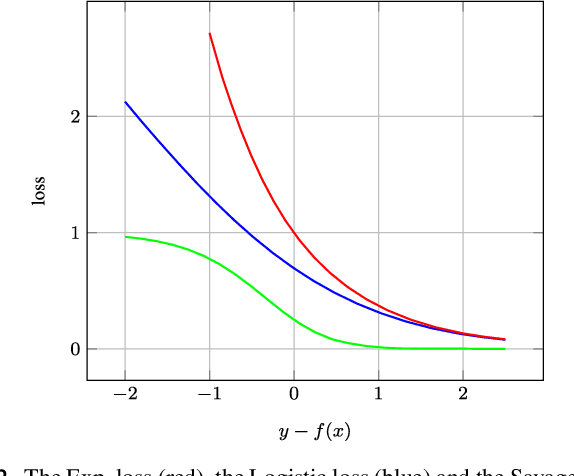
Ensemble techniques are powerful approaches that combine several weak learners to build a stronger one. As a meta-learning framework, ensemble techniques can easily be applied to many machine learning methods. Inspired by ensemble techniques, in this paper we propose an ensemble loss functions applied to a simple regressor. We then propose a half-quadratic learning algorithm in order to find the parameter of the regressor and the optimal weights associated with each loss function. Moreover, we show that our proposed loss function is robust in noisy environments. For a particular class of loss functions, we show that our proposed ensemble loss function is Bayes consistent and robust. Experimental evaluations on several datasets demonstrate that our proposed ensemble loss function significantly improves the performance of a simple regressor in comparison with state-of-the-art methods.

On Extending Neural Networks with Loss Ensembles for Text Classification

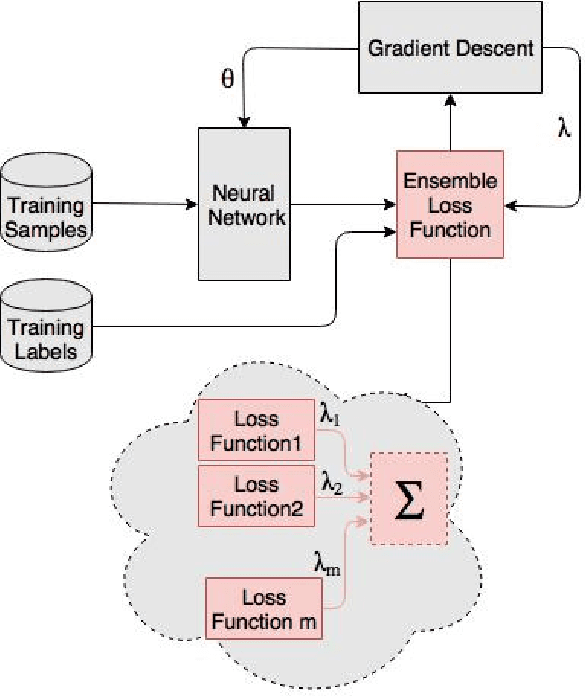
Ensemble techniques are powerful approaches that combine several weak learners to build a stronger one. As a meta learning framework, ensemble techniques can easily be applied to many machine learning techniques. In this paper we propose a neural network extended with an ensemble loss function for text classification. The weight of each weak loss function is tuned within the training phase through the gradient propagation optimization method of the neural network. The approach is evaluated on several text classification datasets. We also evaluate its performance in various environments with several degrees of label noise. Experimental results indicate an improvement of the results and strong resilience against label noise in comparison with other methods.