An Exact Finite-dimensional Explicit Feature Map for Kernel Functions

Kernel methods in machine learning use a kernel function that takes two data points as input and returns their inner product after mapping them to a Hilbert space, implicitly and without actually computing the mapping. For many kernel functions, such as Gaussian and Laplacian kernels, the feature space is known to be infinite-dimensional, making operations in this space possible only implicitly. This implicit nature necessitates algorithms to be expressed using dual representations and the kernel trick. In this paper, given an arbitrary kernel function, we introduce an explicit, finite-dimensional feature map for any arbitrary kernel function that ensures the inner product of data points in the feature space equals the kernel function value, during both training and testing. The existence of this explicit mapping allows for kernelized algorithms to be formulated in their primal form, without the need for the kernel trick or the dual representation. As a first application, we demonstrate how to derive kernelized machine learning algorithms directly, without resorting to the dual representation, and apply this method specifically to PCA. As another application, without any changes to the t-SNE algorithm and its implementation, we use it for visualizing the feature space of kernel functions.

Deep multi-prototype capsule networks

Capsule networks are a type of neural network that identify image parts and form the instantiation parameters of a whole hierarchically. The goal behind the network is to perform an inverse computer graphics task, and the network parameters are the mapping weights that transform parts into a whole. The trainability of capsule networks in complex data with high intra-class or intra-part variation is challenging. This paper presents a multi-prototype architecture for guiding capsule networks to represent the variations in the image parts. To this end, instead of considering a single capsule for each class and part, the proposed method employs several capsules (co-group capsules), capturing multiple prototypes of an object. In the final layer, co-group capsules compete, and their soft output is considered the target for a competitive cross-entropy loss. Moreover, in the middle layers, the most active capsules map to the next layer with a shared weight among the co-groups. Consequently, due to the reduction in parameters, implicit weight-sharing makes it possible to have more deep capsule network layers. The experimental results on MNIST, SVHN, C-Cube, CEDAR, MCYT, and UTSig datasets reveal that the proposed model outperforms others regarding image classification accuracy.

PowerLinear Activation Functions with application to the first layer of CNNs

Convolutional neural networks (CNNs) have become the state-of-the-art tool for dealing with unsolved problems in computer vision and image processing. Since the convolution operator is a linear operator, several generalizations have been proposed to improve the performance of CNNs. One way to increase the capability of the convolution operator is by applying activation functions on the inner product operator. In this paper, we will introduce PowerLinear activation functions, which are based on the polynomial kernel generalization of the convolution operator. EvenPowLin functions are the main branch of the PowerLinear activation functions. This class of activation functions is saturated neither in the positive input region nor in the negative one. Also, the negative inputs are activated with the same magnitude as the positive inputs. These features made the EvenPowLin activation functions able to be utilized in the first layer of CNN architectures and learn complex features of input images. Additionally, EvenPowLin activation functions are used in CNN models to classify the inversion of grayscale images as accurately as the original grayscale images, which is significantly better than commonly used activation functions.

Neural Generalization of Multiple Kernel Learning

Multiple Kernel Learning is a conventional way to learn the kernel function in kernel-based methods. MKL algorithms enhance the performance of kernel methods. However, these methods have a lower complexity compared to deep learning models and are inferior to these models in terms of recognition accuracy. Deep learning models can learn complex functions by applying nonlinear transformations to data through several layers. In this paper, we show that a typical MKL algorithm can be interpreted as a one-layer neural network with linear activation functions. By this interpretation, we propose a Neural Generalization of Multiple Kernel Learning (NGMKL), which extends the conventional multiple kernel learning framework to a multi-layer neural network with nonlinear activation functions. Our experiments on several benchmarks show that the proposed method improves the complexity of MKL algorithms and leads to higher recognition accuracy.

Prototype-based interpretation of the functionality of neurons in winner-take-all neural networks

Prototype-based learning (PbL) using a winner-take-all (WTA) network based on minimum Euclidean distance (ED-WTA) is an intuitive approach to multiclass classification. By constructing meaningful class centers, PbL provides higher interpretability and generalization than hyperplane-based learning (HbL) methods based on maximum Inner Product (IP-WTA) and can efficiently detect and reject samples that do not belong to any classes. In this paper, we first prove the equivalence of IP-WTA and ED-WTA from a representational point of view. Then, we show that naively using this equivalence leads to unintuitive ED-WTA networks in which the centers have high distances to data that they represent. We propose $\pm$ED-WTA which models each neuron with two prototypes: one positive prototype representing samples that are modeled by this neuron and a negative prototype representing the samples that are erroneously won by that neuron during training. We propose a novel training algorithm for the $\pm$ED-WTA network, which cleverly switches between updating the positive and negative prototypes and is essential to the emergence of interpretable prototypes. Unexpectedly, we observed that the negative prototype of each neuron is indistinguishably similar to the positive one. The rationale behind this observation is that the training data that are mistaken with a prototype are indeed similar to it. The main finding of this paper is this interpretation of the functionality of neurons as computing the difference between the distances to a positive and a negative prototype, which is in agreement with the BCM theory. In our experiments, we show that the proposed $\pm$ED-WTA method constructs highly interpretable prototypes that can be successfully used for detecting outlier and adversarial examples.

Improving the Backpropagation Algorithm with Consequentialism Weight Updates over Mini-Batches

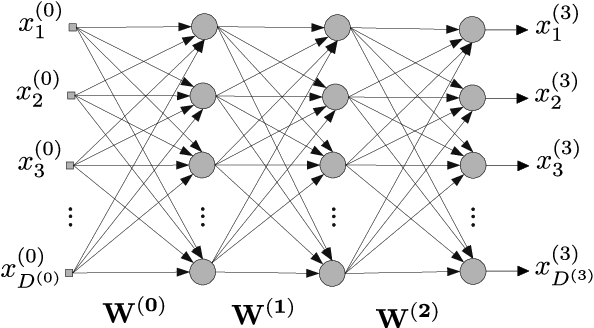
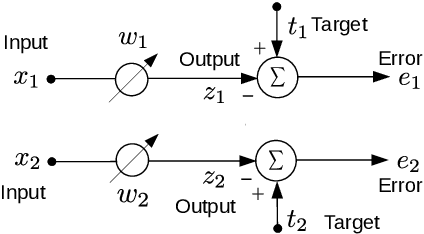
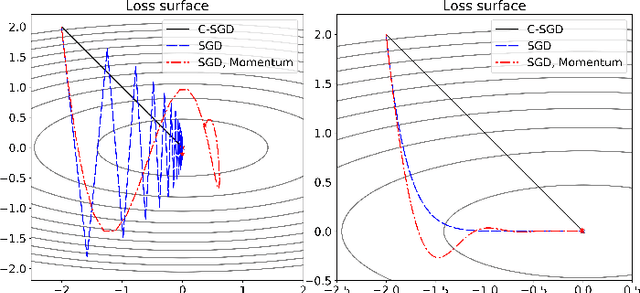
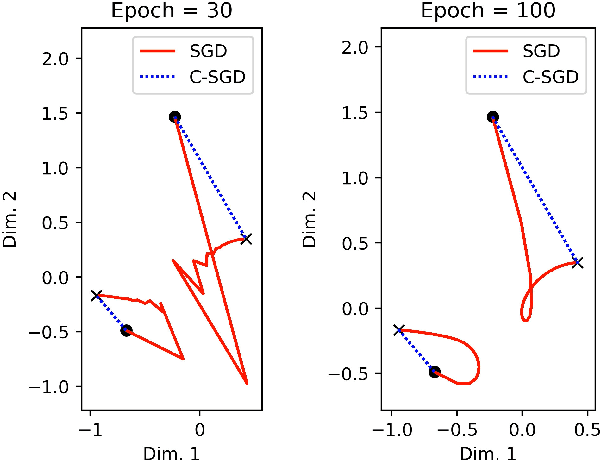
Least mean squares (LMS) is a particular case of the backpropagation (BP) algorithm applied to single-layer neural networks with the mean squared error (MSE) loss. One drawback of the LMS is that the instantaneous weight update is proportional to the square of the norm of the input vector. Normalized least mean squares (NLMS) algorithm amends this drawback by dividing the weight changes by the square of the norm of the input vector. The affine projection algorithm (APA) improved the NLMS algorithm to weight update over a batch of recently seen samples. However, the application of NLMS and APA had been limited to single-layer networks and adaptive filters. In this paper, we consider a virtual target for each neuron of a multi-layer neural network and show that the BP algorithm is equivalent to training the weights of each layer using these virtual targets and the LMS algorithm. We also introduce a consequentialism interpretation of the NLMS and the APA algorithms that justifies their use in multi-layer neural networks. Given any optimization algorithm based on the BP over mini-batches, we propose a novel consequentialism method for updating the weights.Consequently, our proposed weight update can be applied both to plain stochastic gradient descent (SGD) and to momentum methods like RMSProp, Adam, and NAG. These ideas helped us to update the weights more carefully in such a way that minimization of the loss for one sample of the mini-batch does not interfere with other samples in that mini-batch. Our experiments show the usefulness of the proposed method in optimizing deep neural network architectures.

Learning 2D Gabor Filters by Infinite Kernel Learning Regression

Gabor functions have wide-spread applications in image processing and computer vision. In this paper, we prove that 2D Gabor functions are translation-invariant positive-definite kernels and propose a novel formulation for the problem of image representation with Gabor functions based on infinite kernel learning regression. Using this formulation, we obtain a support vector expansion of an image based on a mixture of Gabor functions. The problem with this representation is that all Gabor functions are present at all support vector pixels. Applying LASSO to this support vector expansion, we obtain a sparse representation in which each Gabor function is positioned at a very small set of pixels. As an application, we introduce a method for learning a dataset-specific set of Gabor filters that can be used subsequently for feature extraction. Our experiments show that use of the learned Gabor filters improves the recognition accuracy of a recently introduced face recognition algorithm.

Generalizing the Convolution Operator in Convolutional Neural Networks

Convolutional neural networks have become a main tool for solving many machine vision and machine learning problems. A major element of these networks is the convolution operator which essentially computes the inner product between a weight vector and the vectorized image patches extracted by sliding a window in the image planes of the previous layer. In this paper, we propose two classes of surrogate functions for the inner product operation inherent in the convolution operator and so attain two generalizations of the convolution operator. The first one is the class of positive definite kernel functions where their application is justified by the kernel trick. The second one is the class of similarity measures defined based on a distance function. We justify this by tracing back to the basic idea behind the neocognitron which is the ancestor of CNNs. Both methods are then further generalized by allowing a monotonically increasing function to be applied subsequently. Like any trainable parameter in a neural network, the template pattern and the parameters of the kernel/distance function are trained with the back-propagation algorithm. As an aside, we use the proposed framework to justify the use of sine activation function in CNNs. Our experiments on the MNIST dataset show that the performance of ordinary CNNs can be achieved by generalized CNNs based on weighted L1/L2 distances, proving the applicability of the proposed generalization of the convolutional neural networks.

Training LDCRF model on unsegmented sequences using Connectionist Temporal Classification

Many machine learning problems such as speech recognition, gesture recognition, and handwriting recognition are concerned with simultaneous segmentation and labeling of sequence data. Latent-dynamic conditional random field (LDCRF) is a well-known discriminative method that has been successfully used for this task. However, LDCRF can only be trained with pre-segmented data sequences in which the label of each frame is available apriori. In the realm of neural networks, the invention of connectionist temporal classification (CTC) made it possible to train recurrent neural networks on unsegmented sequences with great success. In this paper, we use CTC to train an LDCRF model on unsegmented sequences. Experimental results on two gesture recognition tasks show that the proposed method outperforms LDCRFs, hidden Markov models, and conditional random fields.

A two-stage learning method for protein-protein interaction prediction

In this paper, a new method for PPI (proteinprotein interaction) prediction is proposed. In PPI prediction, a reliable and sufficient number of training samples is not available, but a large number of unlabeled samples is in hand. In the proposed method, the denoising auto encoders are employed for learning robust features. The obtained robust features are used in order to train a classifier with a better performance. The experimental results demonstrate the capabilities of the proposed method. Protein-protein interaction; Denoising auto encoder;Robust features; Unlabelled data;