Cross-Domain Few-Shot Learning for Hyperspectral Image Classification Based on Mixup Foundation Model

Although cross-domain few-shot learning (CDFSL) for hyper-spectral image (HSI) classification has attracted significant research interest, existing works often rely on an unrealistic data augmentation procedure in the form of external noise to enlarge the sample size, thus greatly simplifying the issue of data scarcity. They involve a large number of parameters for model updates, being prone to the overfitting problem. To the best of our knowledge, none has explored the strength of the foundation model, having strong generalization power to be quickly adapted to downstream tasks. This paper proposes the MIxup FOundation MOdel (MIFOMO) for CDFSL of HSI classifications. MIFOMO is built upon the concept of a remote sensing (RS) foundation model, pre-trained across a large scale of RS problems, thus featuring generalizable features. The notion of coalescent projection (CP) is introduced to quickly adapt the foundation model to downstream tasks while freezing the backbone network. The concept of mixup domain adaptation (MDM) is proposed to address the extreme domain discrepancy problem. Last but not least, the label smoothing concept is implemented to cope with noisy pseudo-label problems. Our rigorous experiments demonstrate the advantage of MIFOMO, where it beats prior arts with up to 14% margin. The source code of MIFOMO is open-sourced in https://github.com/Naeem- Paeedeh/MIFOMO for reproducibility and convenient further study.

Cross-Domain Few-Shot Learning via Adaptive Transformer Networks

Most few-shot learning works rely on the same domain assumption between the base and the target tasks, hindering their practical applications. This paper proposes an adaptive transformer network (ADAPTER), a simple but effective solution for cross-domain few-shot learning where there exist large domain shifts between the base task and the target task. ADAPTER is built upon the idea of bidirectional cross-attention to learn transferable features between the two domains. The proposed architecture is trained with DINO to produce diverse, and less biased features to avoid the supervision collapse problem. Furthermore, the label smoothing approach is proposed to improve the consistency and reliability of the predictions by also considering the predicted labels of the close samples in the embedding space. The performance of ADAPTER is rigorously evaluated in the BSCD-FSL benchmarks in which it outperforms prior arts with significant margins.

Improving the Backpropagation Algorithm with Consequentialism Weight Updates over Mini-Batches

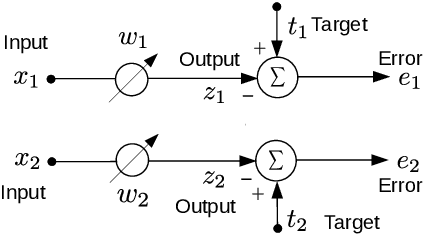
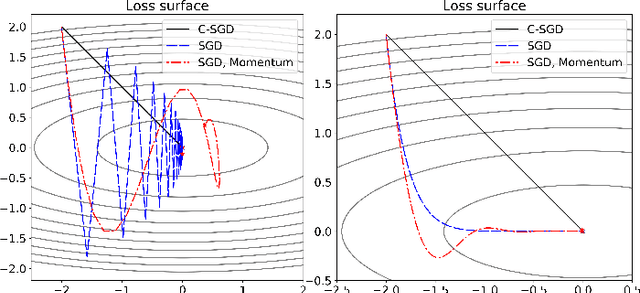
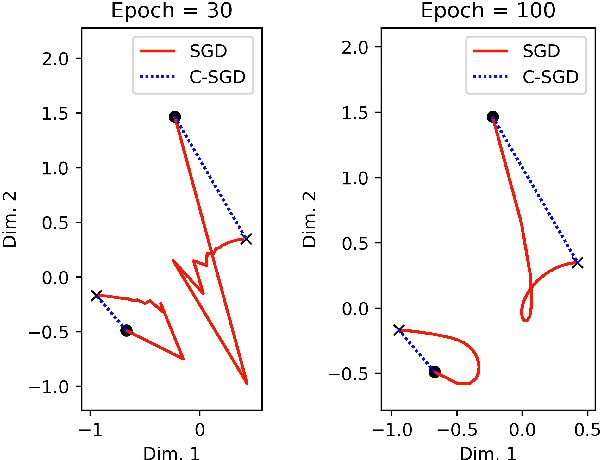
Least mean squares (LMS) is a particular case of the backpropagation (BP) algorithm applied to single-layer neural networks with the mean squared error (MSE) loss. One drawback of the LMS is that the instantaneous weight update is proportional to the square of the norm of the input vector. Normalized least mean squares (NLMS) algorithm amends this drawback by dividing the weight changes by the square of the norm of the input vector. The affine projection algorithm (APA) improved the NLMS algorithm to weight update over a batch of recently seen samples. However, the application of NLMS and APA had been limited to single-layer networks and adaptive filters. In this paper, we consider a virtual target for each neuron of a multi-layer neural network and show that the BP algorithm is equivalent to training the weights of each layer using these virtual targets and the LMS algorithm. We also introduce a consequentialism interpretation of the NLMS and the APA algorithms that justifies their use in multi-layer neural networks. Given any optimization algorithm based on the BP over mini-batches, we propose a novel consequentialism method for updating the weights.Consequently, our proposed weight update can be applied both to plain stochastic gradient descent (SGD) and to momentum methods like RMSProp, Adam, and NAG. These ideas helped us to update the weights more carefully in such a way that minimization of the loss for one sample of the mini-batch does not interfere with other samples in that mini-batch. Our experiments show the usefulness of the proposed method in optimizing deep neural network architectures.