Gemini Robotics: Bringing AI into the Physical World

Recent advancements in large multimodal models have led to the emergence of remarkable generalist capabilities in digital domains, yet their translation to physical agents such as robots remains a significant challenge. This report introduces a new family of AI models purposefully designed for robotics and built upon the foundation of Gemini 2.0. We present Gemini Robotics, an advanced Vision-Language-Action (VLA) generalist model capable of directly controlling robots. Gemini Robotics executes smooth and reactive movements to tackle a wide range of complex manipulation tasks while also being robust to variations in object types and positions, handling unseen environments as well as following diverse, open vocabulary instructions. We show that with additional fine-tuning, Gemini Robotics can be specialized to new capabilities including solving long-horizon, highly dexterous tasks, learning new short-horizon tasks from as few as 100 demonstrations and adapting to completely novel robot embodiments. This is made possible because Gemini Robotics builds on top of the Gemini Robotics-ER model, the second model we introduce in this work. Gemini Robotics-ER (Embodied Reasoning) extends Gemini's multimodal reasoning capabilities into the physical world, with enhanced spatial and temporal understanding. This enables capabilities relevant to robotics including object detection, pointing, trajectory and grasp prediction, as well as multi-view correspondence and 3D bounding box predictions. We show how this novel combination can support a variety of robotics applications. We also discuss and address important safety considerations related to this new class of robotics foundation models. The Gemini Robotics family marks a substantial step towards developing general-purpose robots that realizes AI's potential in the physical world.

Stratified Prediction-Powered Inference for Hybrid Language Model Evaluation

Prediction-powered inference (PPI) is a method that improves statistical estimates based on limited human-labeled data. PPI achieves this by combining small amounts of human-labeled data with larger amounts of data labeled by a reasonably accurate -- but potentially biased -- automatic system, in a way that results in tighter confidence intervals for certain parameters of interest (e.g., the mean performance of a language model). In this paper, we propose a method called Stratified Prediction-Powered Inference (StratPPI), in which we show that the basic PPI estimates can be considerably improved by employing simple data stratification strategies. Without making any assumptions on the underlying automatic labeling system or data distribution, we derive an algorithm for computing provably valid confidence intervals for population parameters (such as averages) that is based on stratified sampling. In particular, we show both theoretically and empirically that, with appropriate choices of stratification and sample allocation, our approach can provide substantially tighter confidence intervals than unstratified approaches. Specifically, StratPPI is expected to improve in cases where the performance of the autorater varies across different conditional distributions of the target data.

Bayesian Prediction-Powered Inference

Prediction-powered inference (PPI) is a method that improves statistical estimates based on limited human-labeled data. Specifically, PPI methods provide tighter confidence intervals by combining small amounts of human-labeled data with larger amounts of data labeled by a reasonably accurate, but potentially biased, automatic system. We propose a framework for PPI based on Bayesian inference that allows researchers to develop new task-appropriate PPI methods easily. Exploiting the ease with which we can design new metrics, we propose improved PPI methods for several importantcases, such as autoraters that give discrete responses (e.g., prompted LLM ``judges'') and autoraters with scores that have a non-linear relationship to human scores.

Scalable Neural Methods for Reasoning With a Symbolic Knowledge Base

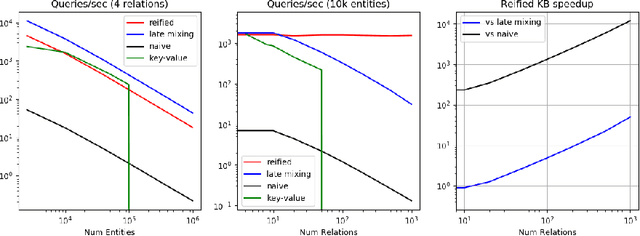
We describe a novel way of representing a symbolic knowledge base (KB) called a sparse-matrix reified KB. This representation enables neural modules that are fully differentiable, faithful to the original semantics of the KB, expressive enough to model multi-hop inferences, and scalable enough to use with realistically large KBs. The sparse-matrix reified KB can be distributed across multiple GPUs, can scale to tens of millions of entities and facts, and is orders of magnitude faster than naive sparse-matrix implementations. The reified KB enables very simple end-to-end architectures to obtain competitive performance on several benchmarks representing two families of tasks: KB completion, and learning semantic parsers from denotations.

Differentiable Representations For Multihop Inference Rules

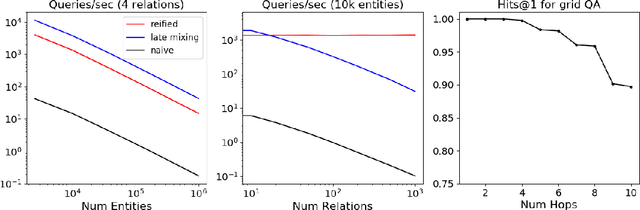
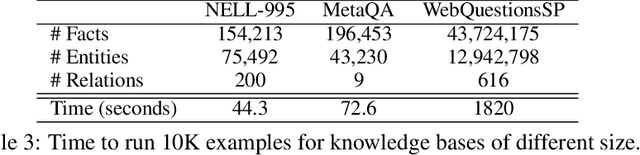
We present efficient differentiable implementations of second-order multi-hop reasoning using a large symbolic knowledge base (KB). We introduce a new operation which can be used to compositionally construct second-order multi-hop templates in a neural model, and evaluate a number of alternative implementations, with different time and memory trade offs. These techniques scale to KBs with millions of entities and tens of millions of triples, and lead to simple models with competitive performance on several learning tasks requiring multi-hop reasoning.