Scalable Neural Methods for Reasoning With a Symbolic Knowledge Base

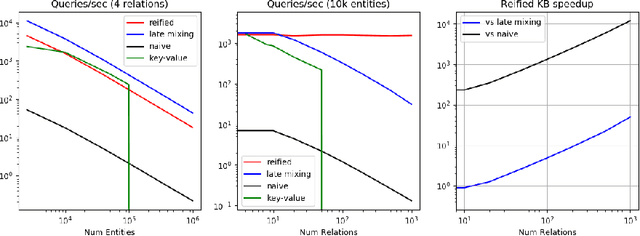
We describe a novel way of representing a symbolic knowledge base (KB) called a sparse-matrix reified KB. This representation enables neural modules that are fully differentiable, faithful to the original semantics of the KB, expressive enough to model multi-hop inferences, and scalable enough to use with realistically large KBs. The sparse-matrix reified KB can be distributed across multiple GPUs, can scale to tens of millions of entities and facts, and is orders of magnitude faster than naive sparse-matrix implementations. The reified KB enables very simple end-to-end architectures to obtain competitive performance on several benchmarks representing two families of tasks: KB completion, and learning semantic parsers from denotations.

Differentiable Representations For Multihop Inference Rules

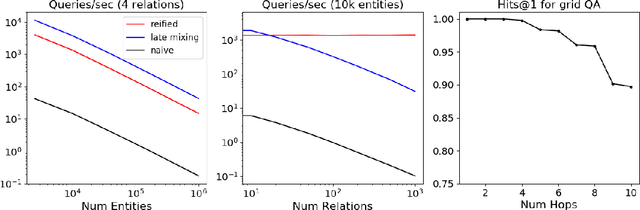
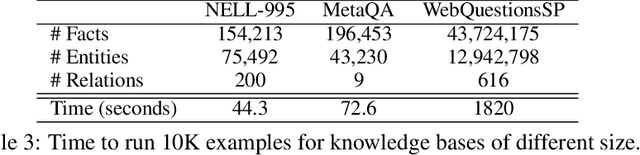
We present efficient differentiable implementations of second-order multi-hop reasoning using a large symbolic knowledge base (KB). We introduce a new operation which can be used to compositionally construct second-order multi-hop templates in a neural model, and evaluate a number of alternative implementations, with different time and memory trade offs. These techniques scale to KBs with millions of entities and tens of millions of triples, and lead to simple models with competitive performance on several learning tasks requiring multi-hop reasoning.

Neural Query Language: A Knowledge Base Query Language for Tensorflow

Large knowledge bases (KBs) are useful for many AI tasks, but are difficult to integrate into modern gradient-based learning systems. Here we describe a framework for accessing soft symbolic database using only differentiable operators. For example, this framework makes it easy to conveniently write neural models that adjust confidences associated with facts in a soft KB; incorporate prior knowledge in the form of hand-coded KB access rules; or learn to instantiate query templates using information extracted from text. NQL can work well with KBs with millions of tuples and hundreds of thousands of entities on a single GPU.