AI-Based Energy Transportation Safety: Pipeline Radial Threat Estimation Using Intelligent Sensing System

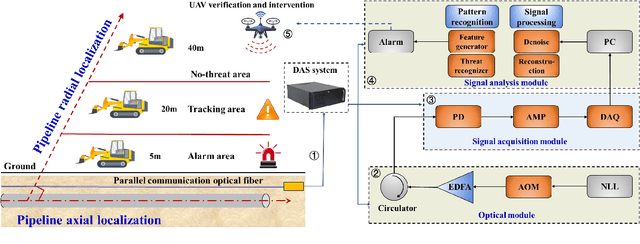
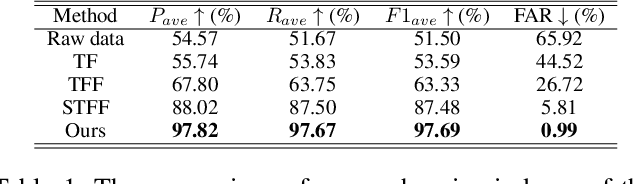
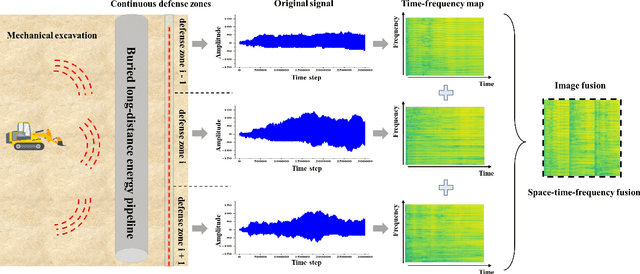
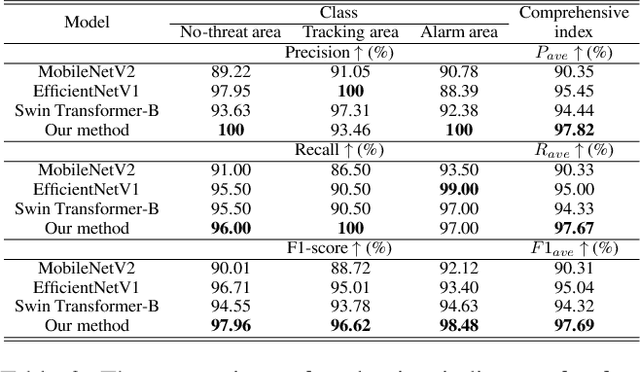
The application of artificial intelligence technology has greatly enhanced and fortified the safety of energy pipelines, particularly in safeguarding against external threats. The predominant methods involve the integration of intelligent sensors to detect external vibration, enabling the identification of event types and locations, thereby replacing manual detection methods. However, practical implementation has exposed a limitation in current methods - their constrained ability to accurately discern the spatial dimensions of external signals, which complicates the authentication of threat events. Our research endeavors to overcome the above issues by harnessing deep learning techniques to achieve a more fine-grained recognition and localization process. This refinement is crucial in effectively identifying genuine threats to pipelines, thus enhancing the safety of energy transportation. This paper proposes a radial threat estimation method for energy pipelines based on distributed optical fiber sensing technology. Specifically, we introduce a continuous multi-view and multi-domain feature fusion methodology to extract comprehensive signal features and construct a threat estimation and recognition network. The utilization of collected acoustic signal data is optimized, and the underlying principle is elucidated. Moreover, we incorporate the concept of transfer learning through a pre-trained model, enhancing both recognition accuracy and training efficiency. Empirical evidence gathered from real-world scenarios underscores the efficacy of our method, notably in its substantial reduction of false alarms and remarkable gains in recognition accuracy. More generally, our method exhibits versatility and can be extrapolated to a broader spectrum of recognition tasks and scenarios.

DBT-DMAE: An Effective Multivariate Time Series Pre-Train Model under Missing Data

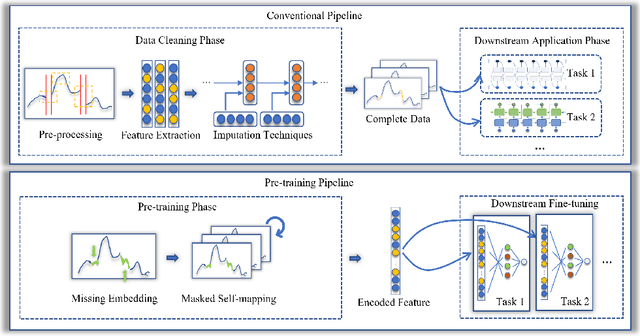
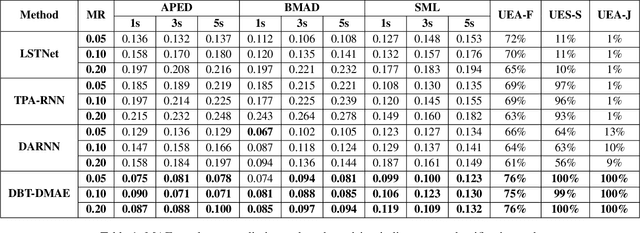
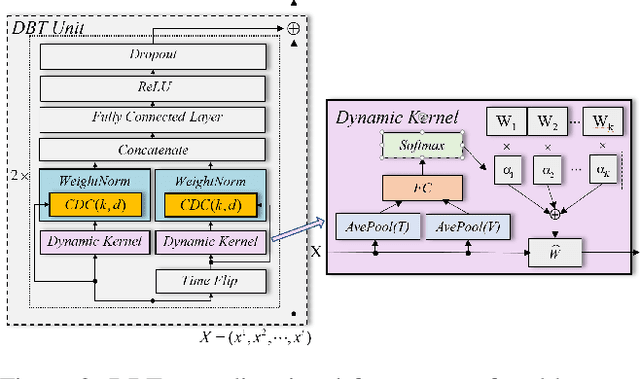
Multivariate time series(MTS) is a universal data type related to many practical applications. However, MTS suffers from missing data problems, which leads to degradation or even collapse of the downstream tasks, such as prediction and classification. The concurrent missing data handling procedures could inevitably arouse the biased estimation and redundancy-training problem when encountering multiple downstream tasks. This paper presents a universally applicable MTS pre-train model, DBT-DMAE, to conquer the abovementioned obstacle. First, a missing representation module is designed by introducing dynamic positional embedding and random masking processing to characterize the missing symptom. Second, we proposed an auto-encoder structure to obtain the generalized MTS encoded representation utilizing an ameliorated TCN structure called dynamic-bidirectional-TCN as the basic unit, which integrates the dynamic kernel and time-fliping trick to draw temporal features effectively. Finally, the overall feed-in and loss strategy is established to ensure the adequate training of the whole model. Comparative experiment results manifest that the DBT-DMAE outperforms the other state-of-the-art methods in six real-world datasets and two different downstream tasks. Moreover, ablation and interpretability experiments are delivered to verify the validity of DBT-DMAE's substructures.

DynamicVAE: Decoupling Reconstruction Error and Disentangled Representation Learning

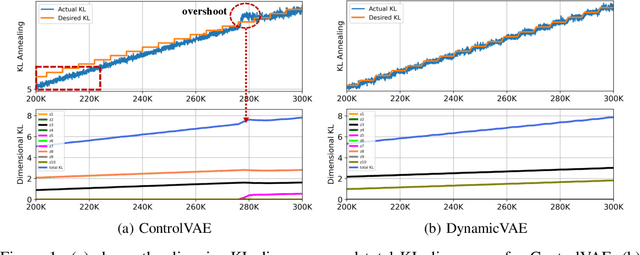
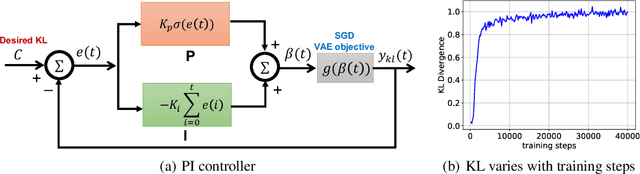
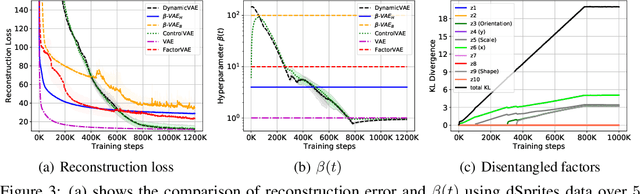
This paper challenges the common assumption that the weight $\beta$, in $\beta$-VAE, should be larger than $1$ in order to effectively disentangle latent factors. We demonstrate that $\beta$-VAE, with $\beta < 1$, can not only attain good disentanglement but also significantly improve reconstruction accuracy via dynamic control. The paper removes the inherent trade-off between reconstruction accuracy and disentanglement for $\beta$-VAE. Existing methods, such as $\beta$-VAE and FactorVAE, assign a large weight to the KL-divergence term in the objective function, leading to high reconstruction errors for the sake of better disentanglement. To mitigate this problem, a ControlVAE has recently been developed that dynamically tunes the KL-divergence weight in an attempt to control the trade-off to more a favorable point. However, ControlVAE fails to eliminate the conflict between the need for a large $\beta$ (for disentanglement) and the need for a small $\beta$. Instead, we propose DynamicVAE that maintains a different $\beta$ at different stages of training, thereby decoupling disentanglement and reconstruction accuracy. In order to evolve the weight, $\beta$, along a trajectory that enables such decoupling, DynamicVAE leverages a modified incremental PI (proportional-integral) controller, and employs a moving average as well as a hybrid annealing method to evolve the value of KL-divergence smoothly in a tightly controlled fashion. We theoretically prove the stability of the proposed approach. Evaluation results on three benchmark datasets demonstrate that DynamicVAE significantly improves the reconstruction accuracy while achieving disentanglement comparable to the best of existing methods. The results verify that our method can separate disentangled representation learning and reconstruction, removing the inherent tension between the two.

Finite-Sample Analysis of Decentralized Temporal-Difference Learning with Linear Function Approximation

Motivated by the emerging use of multi-agent reinforcement learning (MARL) in engineering applications such as networked robotics, swarming drones, and sensor networks, we investigate the policy evaluation problem in a fully decentralized setting, using temporal-difference (TD) learning with linear function approximation to handle large state spaces in practice. The goal of a group of agents is to collaboratively learn the value function of a given policy from locally private rewards observed in a shared environment, through exchanging local estimates with neighbors. Despite their simplicity and widespread use, our theoretical understanding of such decentralized TD learning algorithms remains limited. Existing results were obtained based on i.i.d. data samples, or by imposing an `additional' projection step to control the `gradient' bias incurred by the Markovian observations. In this paper, we provide a finite-sample analysis of the fully decentralized TD(0) learning under both i.i.d. as well as Markovian samples, and prove that all local estimates converge linearly to a small neighborhood of the optimum. The resultant error bounds are the first of its type---in the sense that they hold under the most practical assumptions ---which is made possible by means of a novel multi-step Lyapunov analysis.