GenPlanX. Generation of Plans and Execution

Classical AI Planning techniques generate sequences of actions for complex tasks. However, they lack the ability to understand planning tasks when provided using natural language. The advent of Large Language Models (LLMs) has introduced novel capabilities in human-computer interaction. In the context of planning tasks, LLMs have shown to be particularly good in interpreting human intents among other uses. This paper introduces GenPlanX that integrates LLMs for natural language-based description of planning tasks, with a classical AI planning engine, alongside an execution and monitoring framework. We demonstrate the efficacy of GenPlanX in assisting users with office-related tasks, highlighting its potential to streamline workflows and enhance productivity through seamless human-AI collaboration.

Understanding ProbLog as Probabilistic Argumentation

ProbLog is a popular probabilistic logic programming language/tool, widely used for applications requiring to deal with inherent uncertainties in structured domains. In this paper we study connections between ProbLog and a variant of another well-known formalism combining symbolic reasoning and reasoning under uncertainty, i.e. probabilistic argumentation. Specifically, we show that ProbLog is an instance of a form of Probabilistic Abstract Argumentation (PAA) that builds upon Assumption-Based Argumentation (ABA). The connections pave the way towards equipping ProbLog with alternative semantics, inherited from PAA/PABA, as well as obtaining novel argumentation semantics for PAA/PABA, leveraging on prior connections between ProbLog and argumentation. Further, the connections pave the way towards novel forms of argumentative explanations for ProbLog's outputs.

smProbLog: Stable Model Semantics in ProbLog for Probabilistic Argumentation

Argumentation problems are concerned with determining the acceptability of a set of arguments from their relational structure. When the available information is uncertain, probabilistic argumentation frameworks provide modelling tools to account for it. The first contribution of this paper is a novel interpretation of probabilistic argumentation frameworks as probabilistic logic programs. Probabilistic logic programs are logic programs in which some of the facts are annotated with probabilities. We show that the programs representing probabilistic argumentation frameworks do not satisfy a common assumption in probabilistic logic programming (PLP) semantics, which is, that probabilistic facts fully capture the uncertainty in the domain under investigation. The second contribution of this paper is then a novel PLP semantics for programs where a choice of probabilistic facts does not uniquely determine the truth assignment of the logical atoms. The third contribution of this paper is the implementation of a PLP system supporting this semantics: smProbLog. smProbLog is a novel PLP framework based on the probabilistic logic programming language ProbLog. smProbLog supports many inference and learning tasks typical of PLP, which, together with our first contribution, provide novel reasoning tools for probabilistic argumentation. We evaluate our approach with experiments analyzing the computational cost of the proposed algorithms and their application to a dataset of argumentation problems.

Efficient Knowledge Compilation Beyond Weighted Model Counting

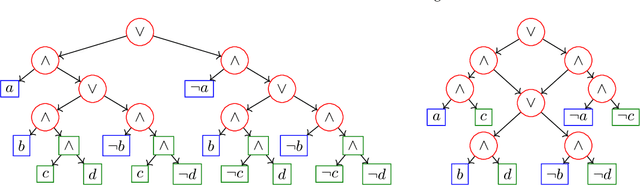
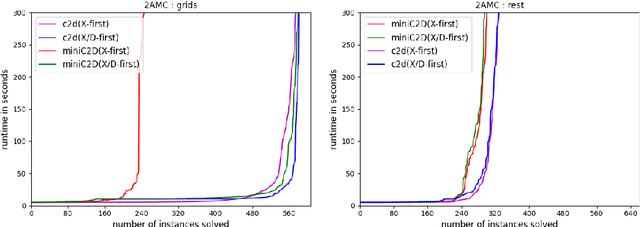
Quantitative extensions of logic programming often require the solution of so called second level inference tasks, i.e., problems that involve a third operation, such as maximization or normalization, on top of addition and multiplication, and thus go beyond the well-known weighted or algebraic model counting setting of probabilistic logic programming under the distribution semantics. We introduce Second Level Algebraic Model Counting (2AMC) as a generic framework for these kinds of problems. As 2AMC is to (algebraic) model counting what forall-exists-SAT is to propositional satisfiability, it is notoriously hard to solve. First level techniques based on Knowledge Compilation (KC) have been adapted for specific 2AMC instances by imposing variable order constraints on the resulting circuit. However, those constraints can severely increase the circuit size and thus decrease the efficiency of such approaches. We show that we can exploit the logical structure of a 2AMC problem to omit parts of these constraints, thus limiting the negative effect. Furthermore, we introduce and implement a strategy to generate a sufficient set of constraints statically, with a priori guarantees for the performance of KC. Our empirical evaluation on several benchmarks and tasks confirms that our theoretical results can translate into more efficient solving in practice. Under consideration for acceptance in TPLP.

SMProbLog: Stable Model Semantics in ProbLog and its Applications in Argumentation

We introduce SMProbLog, a generalization of the probabilistic logic programming language ProbLog. A ProbLog program defines a distribution over logic programs by specifying for each clause the probability that it belongs to a randomly sampled program, and these probabilities are mutually independent. The semantics of ProbLog is given by the success probability of a query, which corresponds to the probability that the query succeeds in a randomly sampled program. It is well-defined when each random sample uniquely determines the truth values of all logical atoms. Argumentation problems, however, represent an interesting practical application where this is not always the case. SMProbLog generalizes the semantics of ProbLog to the setting where multiple truth assignments are possible for a randomly sampled program, and implements the corresponding algorithms for both inference and learning tasks. We then show how this novel framework can be used to reason about probabilistic argumentation problems. Therefore, the key contribution of this paper are: a more general semantics for ProbLog programs, its implementation into a probabilistic programming framework for both inference and parameter learning, and a novel approach to probabilistic argumentation problems based on such framework.