Solving Decision Theory Problems with Probabilistic Answer Set Programming

Solving a decision theory problem usually involves finding the actions, among a set of possible ones, which optimize the expected reward, possibly accounting for the uncertainty of the environment. In this paper, we introduce the possibility to encode decision theory problems with Probabilistic Answer Set Programming under the credal semantics via decision atoms and utility attributes. To solve the task we propose an algorithm based on three layers of Algebraic Model Counting, that we test on several synthetic datasets against an algorithm that adopts answer set enumeration. Empirical results show that our algorithm can manage non trivial instances of programs in a reasonable amount of time. Under consideration in Theory and Practice of Logic Programming (TPLP).

Extended Version of: On the Structural Hardness of Answer Set Programming: Can Structure Efficiently Confine the Power of Disjunctions?

Answer Set Programming (ASP) is a generic problem modeling and solving framework with a strong focus on knowledge representation and a rapid growth of industrial applications. So far, the study of complexity resulted in characterizing hardness and determining their sources, fine-grained insights in the form of dichotomy-style results, as well as detailed parameterized complexity landscapes. Unfortunately, for the well-known parameter treewidth disjunctive programs require double-exponential runtime under reasonable complexity assumptions. This quickly becomes out of reach. We deal with the classification of structural parameters for disjunctive ASP on the program's rule structure (incidence graph). First, we provide a polynomial kernel to obtain single-exponential runtime in terms of vertex cover size, despite subset-minimization being not represented in the program's structure. Then we turn our attention to strictly better structural parameters between vertex cover size and treewidth. Here, we provide double-exponential lower bounds for the most prominent parameters in that range: treedepth, feedback vertex size, and cliquewidth. Based on this, we argue that unfortunately our options beyond vertex cover size are limited. Our results provide an in-depth hardness study, relying on a novel reduction from normal to disjunctive programs, trading the increase of complexity for an exponential parameter compression.

"What if?" in Probabilistic Logic Programming

A ProbLog program is a logic program with facts that only hold with a specified probability. In this contribution we extend this ProbLog language by the ability to answer "What if" queries. Intuitively, a ProbLog program defines a distribution by solving a system of equations in terms of mutually independent predefined Boolean random variables. In the theory of causality, Judea Pearl proposes a counterfactual reasoning for such systems of equations. Based on Pearl's calculus, we provide a procedure for processing these counterfactual queries on ProbLog programs, together with a proof of correctness and a full implementation. Using the latter, we provide insights into the influence of different parameters on the scalability of inference. Finally, we also show that our approach is consistent with CP-logic, i.e. with the causal semantics for logic programs with annotated with disjunctions.

Contextual Reasoning for Scene Generation (Technical Report)

We present a continuation to our previous work, in which we developed the MR-CKR framework to reason with knowledge overriding across contexts organized in multi-relational hierarchies. Reasoning is realized via ASP with algebraic measures, allowing for flexible definitions of preferences. In this paper, we show how to apply our theoretical work to real autonomous-vehicle scene data. Goal of this work is to apply MR-CKR to the problem of generating challenging scenes for autonomous vehicle learning. In practice, most of the scene data for AV learning models common situations, thus it might be difficult to capture cases where a particular situation occurs (e.g. partial occlusions of a crossing pedestrian). The MR-CKR model allows for data organization exploiting the multi-dimensionality of such data (e.g., temporal and spatial). Reasoning over multiple contexts enables the verification and configuration of scenes, using the combination of different scene ontologies. We describe a framework for semantically guided data generation, based on a combination of MR-CKR and Algebraic Measures. The framework is implemented in a proof-of-concept prototype exemplifying some cases of scene generation.

Efficient Knowledge Compilation Beyond Weighted Model Counting

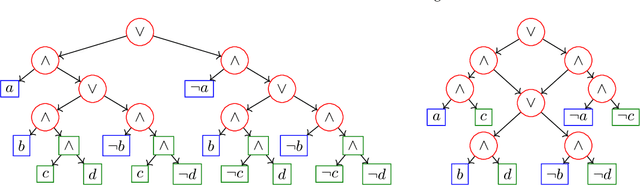
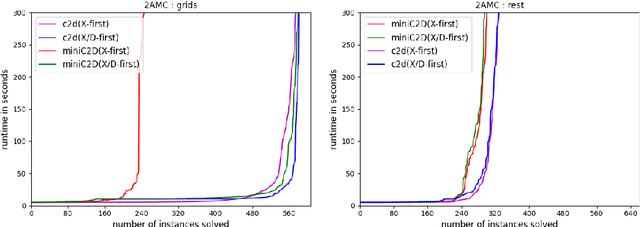
Quantitative extensions of logic programming often require the solution of so called second level inference tasks, i.e., problems that involve a third operation, such as maximization or normalization, on top of addition and multiplication, and thus go beyond the well-known weighted or algebraic model counting setting of probabilistic logic programming under the distribution semantics. We introduce Second Level Algebraic Model Counting (2AMC) as a generic framework for these kinds of problems. As 2AMC is to (algebraic) model counting what forall-exists-SAT is to propositional satisfiability, it is notoriously hard to solve. First level techniques based on Knowledge Compilation (KC) have been adapted for specific 2AMC instances by imposing variable order constraints on the resulting circuit. However, those constraints can severely increase the circuit size and thus decrease the efficiency of such approaches. We show that we can exploit the logical structure of a 2AMC problem to omit parts of these constraints, thus limiting the negative effect. Furthermore, we introduce and implement a strategy to generate a sufficient set of constraints statically, with a priori guarantees for the performance of KC. Our empirical evaluation on several benchmarks and tasks confirms that our theoretical results can translate into more efficient solving in practice. Under consideration for acceptance in TPLP.

Quantitative and Stream Extensions of Answer Set Programming

Answer Set Programming has separately been extended with constraints, to the streaming domain, and with capabilities to reason over the quantities associated with answer sets. We propose the introduction and analysis of a general framework that incorporates all three directions of extension by exploiting the strengths of Here-and-There Logic and Weighted Logic.

Reasoning on Multi-Relational Contextual Hierarchies via Answer Set Programming with Algebraic Measures

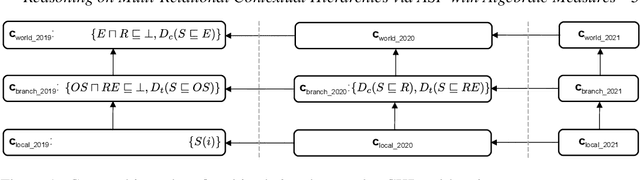
Dealing with context dependent knowledge has led to different formalizations of the notion of context. Among them is the Contextualized Knowledge Repository (CKR) framework, which is rooted in description logics but links on the reasoning side strongly to logic programs and Answer Set Programming (ASP) in particular. The CKR framework caters for reasoning with defeasible axioms and exceptions in contexts, which was extended to knowledge inheritance across contexts in a coverage (specificity) hierarchy. However, the approach supports only this single type of contextual relation and the reasoning procedures work only for restricted hierarchies, due to non-trivial issues with model preference under exceptions. In this paper, we overcome these limitations and present a generalization of CKR hierarchies to multiple contextual relations, along with their interpretation of defeasible axioms and preference. To support reasoning, we use ASP with algebraic measures, which is a recent extension of ASP with weighted formulas over semirings that allows one to associate quantities with interpretations depending on the truth values of propositional atoms. Notably, we show that for a relevant fragment of CKR hierarchies with multiple contextual relations, query answering can be realized with the popular asprin framework. The algebraic measures approach is more powerful and enables e.g. reasoning with epistemic queries over CKRs, which opens interesting perspectives for the use of quantitative ASP extensions in other applications. Under consideration for acceptance in Theory and Practice of Logic Programming (TPLP).

ASP(AC): Answer Set Programming with Algebraic Constraints

Weighted Logic is a powerful tool for the specification of calculations over semirings that depend on qualitative information. Using a novel combination of Weighted Logic and Here-and-There (HT) Logic, in which this dependence is based on intuitionistic grounds, we introduce Answer Set Programming with Algebraic Constraints (ASP(AC)), where rules may contain constraints that compare semiring values to weighted formula evaluations. Such constraints provide streamlined access to a manifold of constructs available in ASP, like aggregates, choice constraints, and arithmetic operators. They extend some of them and provide a generic framework for defining programs with algebraic computation, which can be fruitfully used e.g. for provenance semantics of datalog programs. While undecidable in general, expressive fragments of ASP(AC) can be exploited for effective problem-solving in a rich framework. This work is under consideration for acceptance in Theory and Practice of Logic Programming.