Philip Marcus
MeshfreeFlowNet: A Physics-Constrained Deep Continuous Space-Time Super-Resolution Framework
May 01, 2020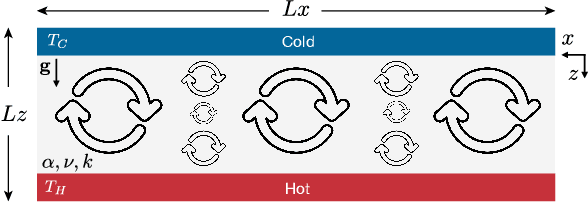
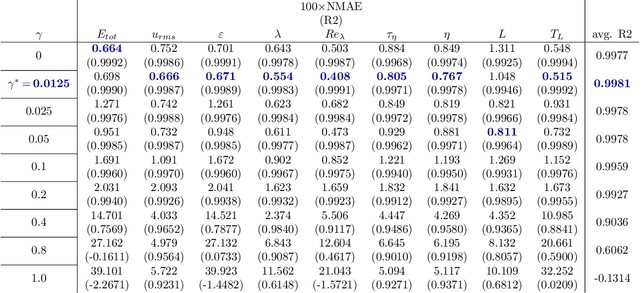
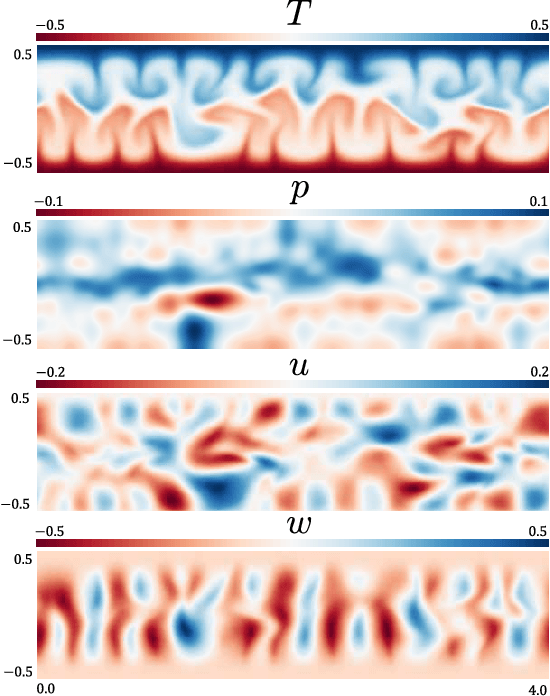
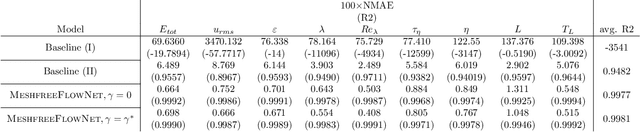
Abstract:We propose MeshfreeFlowNet, a novel deep learning-based super-resolution framework to generate continuous (grid-free) spatio-temporal solutions from the low-resolution inputs. While being computationally efficient, MeshfreeFlowNet accurately recovers the fine-scale quantities of interest. MeshfreeFlowNet allows for: (i) the output to be sampled at all spatio-temporal resolutions, (ii) a set of Partial Differential Equation (PDE) constraints to be imposed, and (iii) training on fixed-size inputs on arbitrarily sized spatio-temporal domains owing to its fully convolutional encoder. We empirically study the performance of MeshfreeFlowNet on the task of super-resolution of turbulent flows in the Rayleigh-Benard convection problem. Across a diverse set of evaluation metrics, we show that MeshfreeFlowNet significantly outperforms existing baselines. Furthermore, we provide a large scale implementation of MeshfreeFlowNet and show that it efficiently scales across large clusters, achieving 96.80% scaling efficiency on up to 128 GPUs and a training time of less than 4 minutes.
DDSL: Deep Differentiable Simplex Layer for Learning Geometric Signals
Mar 22, 2019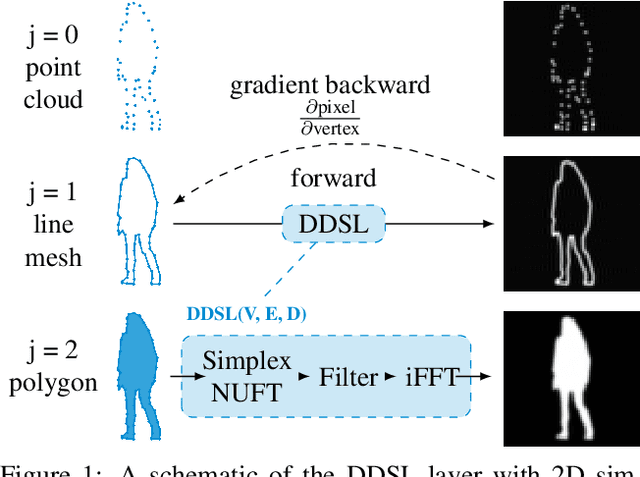

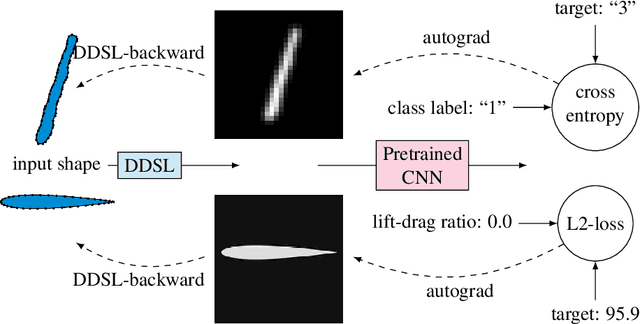

Abstract:We present a Deep Differentiable Simplex Layer (DDSL) for neural networks for geometric deep learning. The DDSL is a differentiable layer compatible with deep neural networks for bridging simplex mesh-based geometry representations (point clouds, line mesh, triangular mesh, tetrahedral mesh) with raster images (e.g., 2D/3D grids). The DDSL uses Non-Uniform Fourier Transform (NUFT) to perform differentiable, efficient, anti-aliased rasterization of simplex-based signals. We present a complete theoretical framework for the process as well as an efficient backpropagation algorithm. Compared to previous differentiable renderers and rasterizers, the DDSL generalizes to arbitrary simplex degrees and dimensions. In particular, we explore its applications to 2D shapes and illustrate two applications of this method: (1) mesh editing and optimization guided by neural network outputs, and (2) using DDSL for a differentiable rasterization loss to facilitate end-to-end training of polygon generators. We are able to validate the effectiveness of gradient-based shape optimization with the example of airfoil optimization, and using the differentiable rasterization loss to facilitate end-to-end training, we surpass state of the art for polygonal image segmentation given ground-truth bounding boxes.
Convolutional Neural Networks on non-uniform geometrical signals using Euclidean spectral transformation
Jan 07, 2019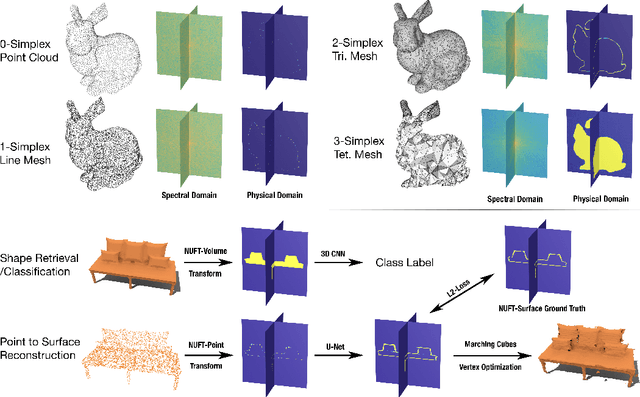
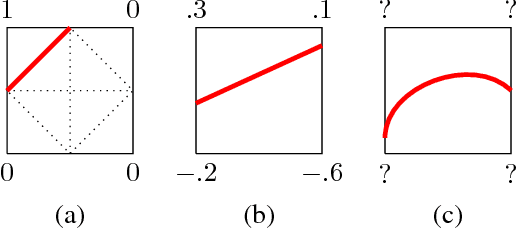
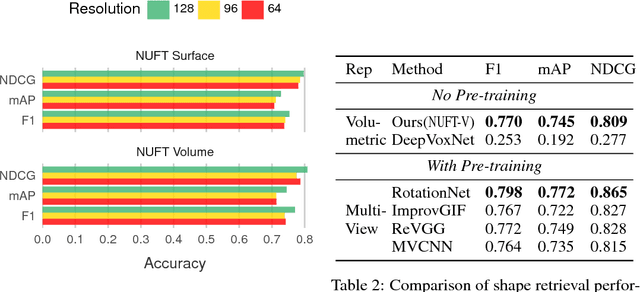
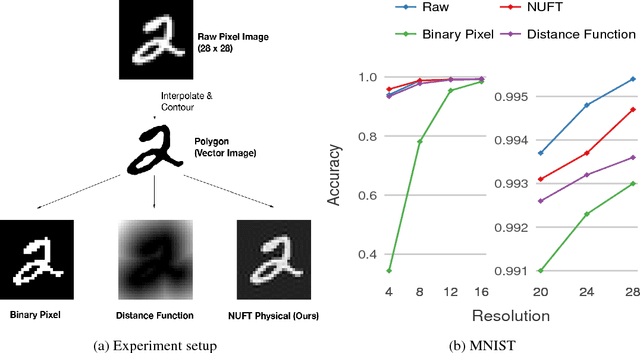
Abstract:Convolutional Neural Networks (CNN) have been successful in processing data signals that are uniformly sampled in the spatial domain (e.g., images). However, most data signals do not natively exist on a grid, and in the process of being sampled onto a uniform physical grid suffer significant aliasing error and information loss. Moreover, signals can exist in different topological structures as, for example, points, lines, surfaces and volumes. It has been challenging to analyze signals with mixed topologies (for example, point cloud with surface mesh). To this end, we develop mathematical formulations for Non-Uniform Fourier Transforms (NUFT) to directly, and optimally, sample nonuniform data signals of different topologies defined on a simplex mesh into the spectral domain with no spatial sampling error. The spectral transform is performed in the Euclidean space, which removes the translation ambiguity from works on the graph spectrum. Our representation has four distinct advantages: (1) the process causes no spatial sampling error during the initial sampling, (2) the generality of this approach provides a unified framework for using CNNs to analyze signals of mixed topologies, (3) it allows us to leverage state-of-the-art backbone CNN architectures for effective learning without having to design a particular architecture for a particular data structure in an ad-hoc fashion, and (4) the representation allows weighted meshes where each element has a different weight (i.e., texture) indicating local properties. We achieve results on par with the state-of-the-art for the 3D shape retrieval task, and a new state-of-the-art for the point cloud to surface reconstruction task.
Spherical CNNs on Unstructured Grids
Jan 07, 2019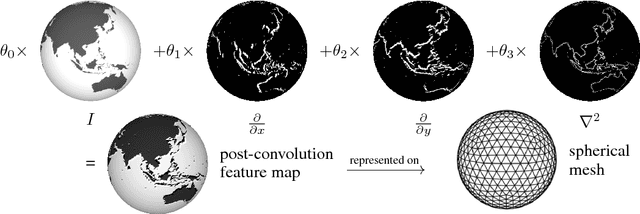
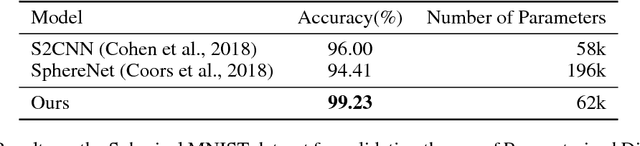
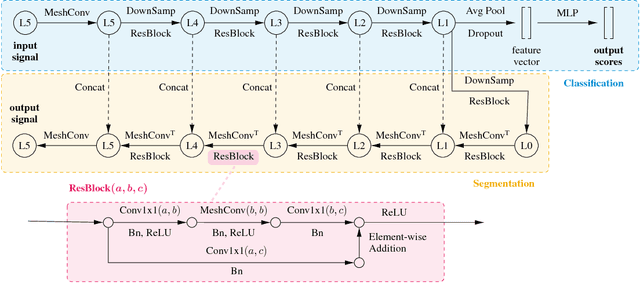

Abstract:We present an efficient convolution kernel for Convolutional Neural Networks (CNNs) on unstructured grids using parameterized differential operators while focusing on spherical signals such as panorama images or planetary signals. To this end, we replace conventional convolution kernels with linear combinations of differential operators that are weighted by learnable parameters. Differential operators can be efficiently estimated on unstructured grids using one-ring neighbors, and learnable parameters can be optimized through standard back-propagation. As a result, we obtain extremely efficient neural networks that match or outperform state-of-the-art network architectures in terms of performance but with a significantly lower number of network parameters. We evaluate our algorithm in an extensive series of experiments on a variety of computer vision and climate science tasks, including shape classification, climate pattern segmentation, and omnidirectional image semantic segmentation. Overall, we present (1) a novel CNN approach on unstructured grids using parameterized differential operators for spherical signals, and (2) we show that our unique kernel parameterization allows our model to achieve the same or higher accuracy with significantly fewer network parameters.
Hierarchical Detail Enhancing Mesh-Based Shape Generation with 3D Generative Adversarial Network
Sep 22, 2017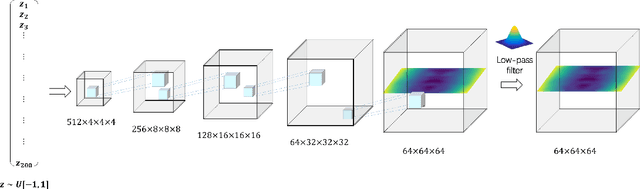

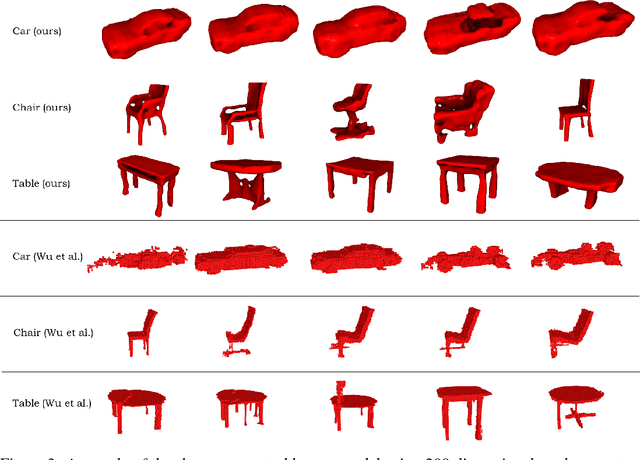

Abstract:Automatic mesh-based shape generation is of great interest across a wide range of disciplines, from industrial design to gaming, computer graphics and various other forms of digital art. While most traditional methods focus on primitive based model generation, advances in deep learning made it possible to learn 3-dimensional geometric shape representations in an end-to-end manner. However, most current deep learning based frameworks focus on the representation and generation of voxel and point-cloud based shapes, making it not directly applicable to design and graphics communities. This study addresses the needs for automatic generation of mesh-based geometries, and propose a novel framework that utilizes signed distance function representation that generates detail preserving three-dimensional surface mesh by a deep learning based approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge