Gated Linear Networks

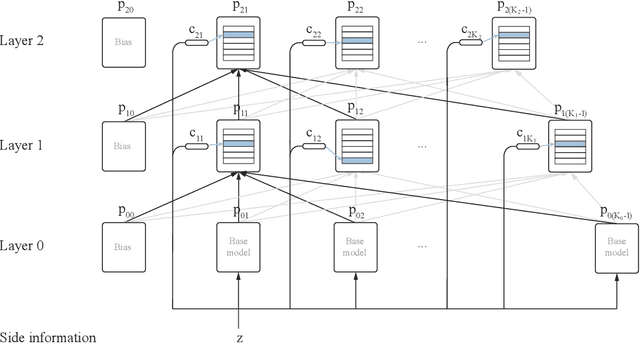
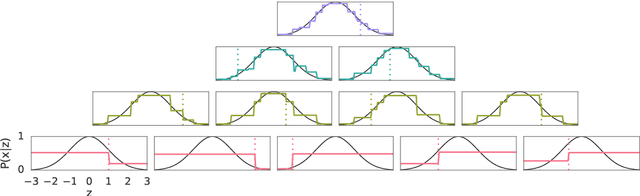
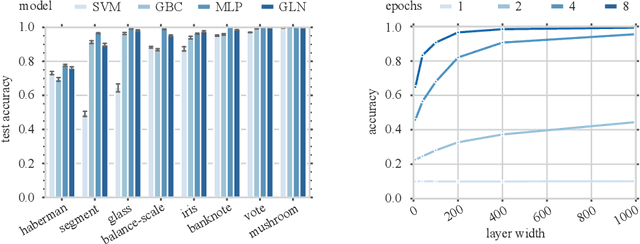
This paper presents a family of backpropagation-free neural architectures, Gated Linear Networks (GLNs),that are well suited to online learning applications where sample efficiency is of paramount importance. The impressive empirical performance of these architectures has long been known within the data compression community, but a theoretically satisfying explanation as to how and why they perform so well has proven difficult. What distinguishes these architectures from other neural systems is the distributed and local nature of their credit assignment mechanism; each neuron directly predicts the target and has its own set of hard-gated weights that are locally adapted via online convex optimization. By providing an interpretation, generalization and subsequent theoretical analysis, we show that sufficiently large GLNs are universal in a strong sense: not only can they model any compactly supported, continuous density function to arbitrary accuracy, but that any choice of no-regret online convex optimization technique will provably converge to the correct solution with enough data. Empirically we show a collection of single-pass learning results on established machine learning benchmarks that are competitive with results obtained with general purpose batch learning techniques.

Hamiltonian Generative Networks

The Hamiltonian formalism plays a central role in classical and quantum physics. Hamiltonians are the main tool for modelling the continuous time evolution of systems with conserved quantities, and they come equipped with many useful properties, like time reversibility and smooth interpolation in time. These properties are important for many machine learning problems - from sequence prediction to reinforcement learning and density modelling - but are not typically provided out of the box by standard tools such as recurrent neural networks. In this paper, we introduce the Hamiltonian Generative Network (HGN), the first approach capable of consistently learning Hamiltonian dynamics from high-dimensional observations (such as images) without restrictive domain assumptions. Once trained, we can use HGN to sample new trajectories, perform rollouts both forward and backward in time and even speed up or slow down the learned dynamics. We demonstrate how a simple modification of the network architecture turns HGN into a powerful normalising flow model, called Neural Hamiltonian Flow (NHF), that uses Hamiltonian dynamics to model expressive densities. We hope that our work serves as a first practical demonstration of the value that the Hamiltonian formalism can bring to deep learning.

Equivariant Hamiltonian Flows

This paper introduces equivariant hamiltonian flows, a method for learning expressive densities that are invariant with respect to a known Lie-algebra of local symmetry transformations while providing an equivariant representation of the data. We provide proof of principle demonstrations of how such flows can be learnt, as well as how the addition of symmetry invariance constraints can improve data efficiency and generalisation. Finally, we make connections to disentangled representation learning and show how this work relates to a recently proposed definition.

Online Learning with Gated Linear Networks

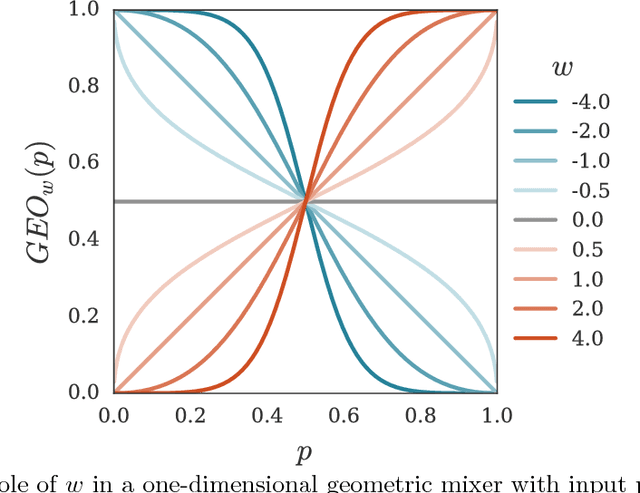
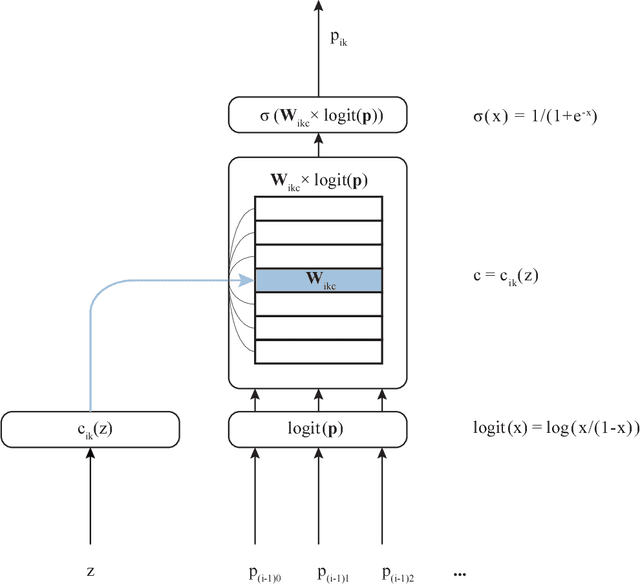
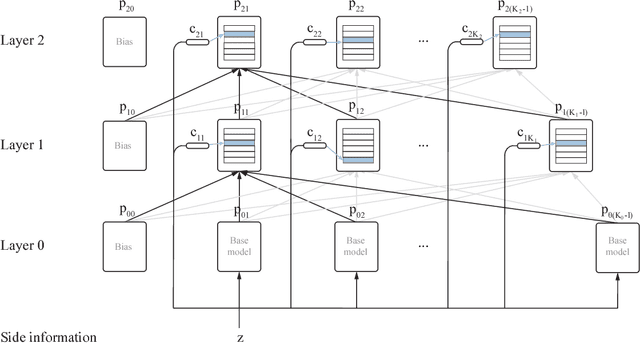
This paper describes a family of probabilistic architectures designed for online learning under the logarithmic loss. Rather than relying on non-linear transfer functions, our method gains representational power by the use of data conditioning. We state under general conditions a learnable capacity theorem that shows this approach can in principle learn any bounded Borel-measurable function on a compact subset of euclidean space; the result is stronger than many universality results for connectionist architectures because we provide both the model and the learning procedure for which convergence is guaranteed.

Criticality & Deep Learning II: Momentum Renormalisation Group

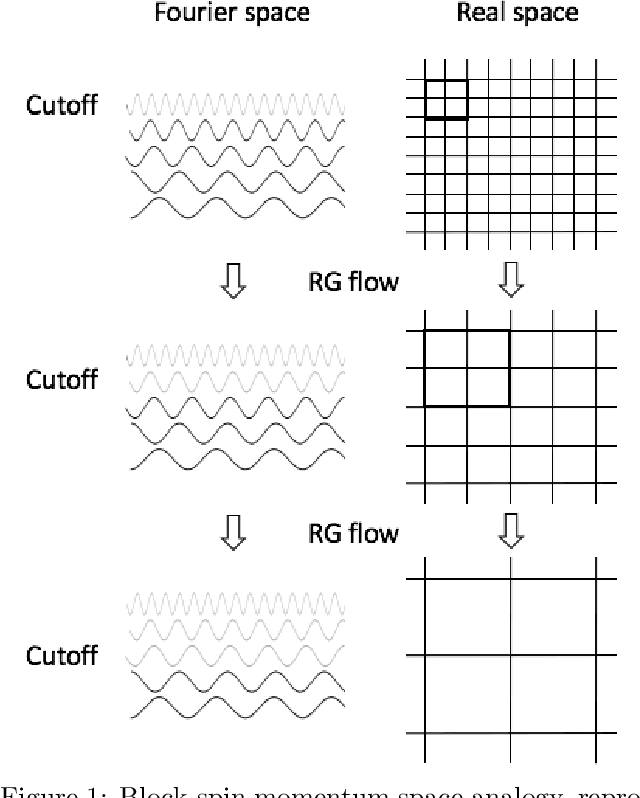
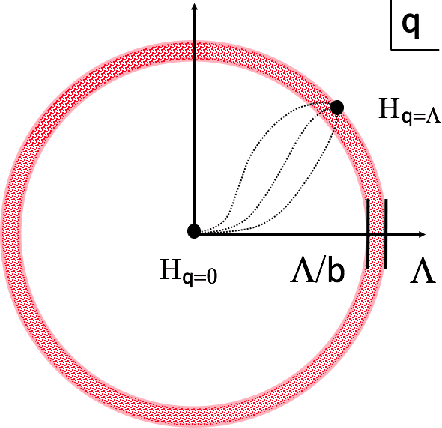
Guided by critical systems found in nature we develop a novel mechanism consisting of inhomogeneous polynomial regularisation via which we can induce scale invariance in deep learning systems. Technically, we map our deep learning (DL) setup to a genuine field theory, on which we act with the Renormalisation Group (RG) in momentum space and produce the flow equations of the couplings; those are translated to constraints and consequently interpreted as "critical regularisation" conditions in the optimiser; the resulting equations hence prove to be sufficient conditions for - and serve as an elegant and simple mechanism to induce scale invariance in any deep learning setup.

Criticality & Deep Learning I: Generally Weighted Nets

Motivated by the idea that criticality and universality of phase transitions might play a crucial role in achieving and sustaining learning and intelligent behaviour in biological and artificial networks, we analyse a theoretical and a pragmatic experimental set up for critical phenomena in deep learning. On the theoretical side, we use results from statistical physics to carry out critical point calculations in feed-forward/fully connected networks, while on the experimental side we set out to find traces of criticality in deep neural networks. This is our first step in a series of upcoming investigations to map out the relationship between criticality and learning in deep networks.