Criticality & Deep Learning II: Momentum Renormalisation Group

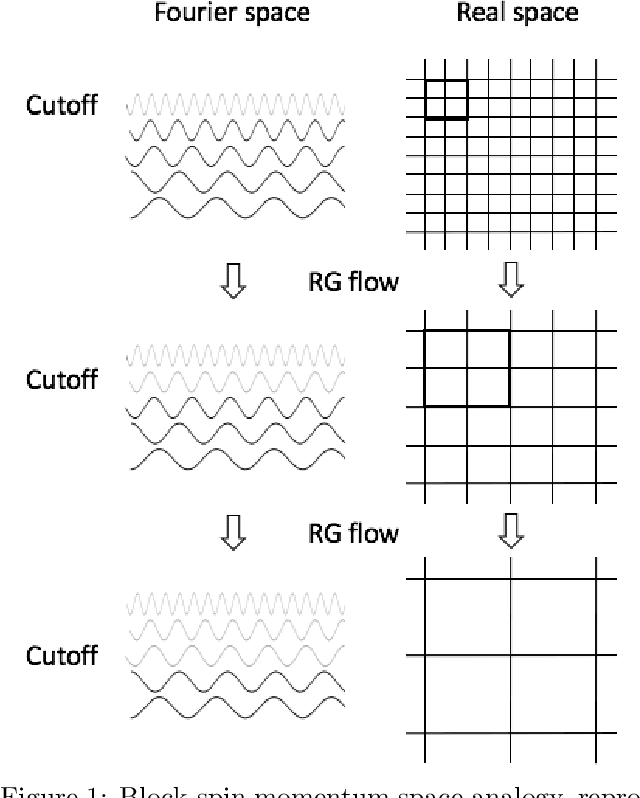
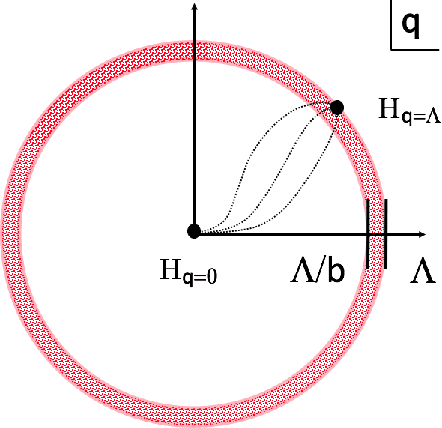
Guided by critical systems found in nature we develop a novel mechanism consisting of inhomogeneous polynomial regularisation via which we can induce scale invariance in deep learning systems. Technically, we map our deep learning (DL) setup to a genuine field theory, on which we act with the Renormalisation Group (RG) in momentum space and produce the flow equations of the couplings; those are translated to constraints and consequently interpreted as "critical regularisation" conditions in the optimiser; the resulting equations hence prove to be sufficient conditions for - and serve as an elegant and simple mechanism to induce scale invariance in any deep learning setup.

Criticality & Deep Learning I: Generally Weighted Nets

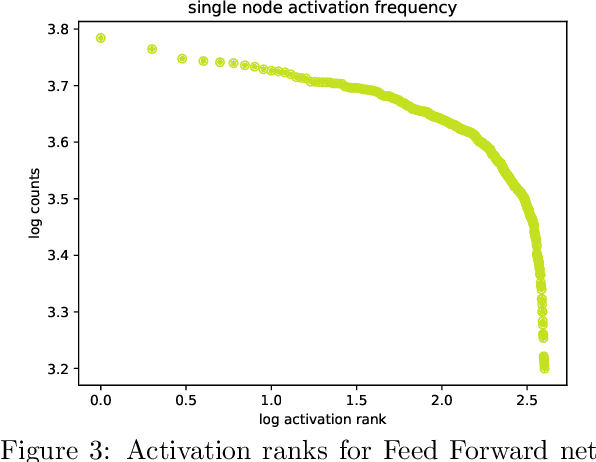
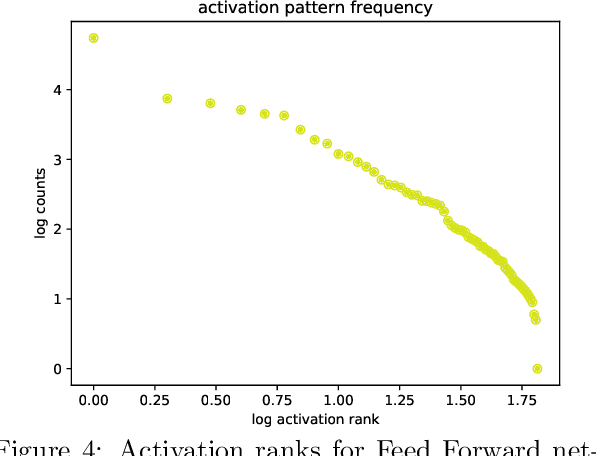
Motivated by the idea that criticality and universality of phase transitions might play a crucial role in achieving and sustaining learning and intelligent behaviour in biological and artificial networks, we analyse a theoretical and a pragmatic experimental set up for critical phenomena in deep learning. On the theoretical side, we use results from statistical physics to carry out critical point calculations in feed-forward/fully connected networks, while on the experimental side we set out to find traces of criticality in deep neural networks. This is our first step in a series of upcoming investigations to map out the relationship between criticality and learning in deep networks.