Learning Universal Predictors

Meta-learning has emerged as a powerful approach to train neural networks to learn new tasks quickly from limited data. Broad exposure to different tasks leads to versatile representations enabling general problem solving. But, what are the limits of meta-learning? In this work, we explore the potential of amortizing the most powerful universal predictor, namely Solomonoff Induction (SI), into neural networks via leveraging meta-learning to its limits. We use Universal Turing Machines (UTMs) to generate training data used to expose networks to a broad range of patterns. We provide theoretical analysis of the UTM data generation processes and meta-training protocols. We conduct comprehensive experiments with neural architectures (e.g. LSTMs, Transformers) and algorithmic data generators of varying complexity and universality. Our results suggest that UTM data is a valuable resource for meta-learning, and that it can be used to train neural networks capable of learning universal prediction strategies.

Language Modeling Is Compression

It has long been established that predictive models can be transformed into lossless compressors and vice versa. Incidentally, in recent years, the machine learning community has focused on training increasingly large and powerful self-supervised (language) models. Since these large language models exhibit impressive predictive capabilities, they are well-positioned to be strong compressors. In this work, we advocate for viewing the prediction problem through the lens of compression and evaluate the compression capabilities of large (foundation) models. We show that large language models are powerful general-purpose predictors and that the compression viewpoint provides novel insights into scaling laws, tokenization, and in-context learning. For example, Chinchilla 70B, while trained primarily on text, compresses ImageNet patches to 43.4% and LibriSpeech samples to 16.4% of their raw size, beating domain-specific compressors like PNG (58.5%) or FLAC (30.3%), respectively. Finally, we show that the prediction-compression equivalence allows us to use any compressor (like gzip) to build a conditional generative model.

Hierarchical Partitioning Forecaster

In this work we consider a new family of algorithms for sequential prediction, Hierarchical Partitioning Forecasters (HPFs). Our goal is to provide appealing theoretical - regret guarantees on a powerful model class - and practical - empirical performance comparable to deep networks - properties at the same time. We built upon three principles: hierarchically partitioning the feature space into sub-spaces, blending forecasters specialized to each sub-space and learning HPFs via local online learning applied to these individual forecasters. Following these principles allows us to obtain regret guarantees, where Constant Partitioning Forecasters (CPFs) serve as competitor. A CPF partitions the feature space into sub-spaces and predicts with a fixed forecaster per sub-space. Fixing a hierarchical partition $\mathcal H$ and considering any CPF with a partition that can be constructed using elements of $\mathcal H$ we provide two guarantees: first, a generic one that unveils how local online learning determines regret of learning the entire HPF online; second, a concrete instance that considers HPF with linear forecasters (LHPF) and exp-concave losses where we obtain $O(k \log T)$ regret for sequences of length $T$ where $k$ is a measure of complexity for the competing CPF. Finally, we provide experiments that compare LHPF to various baselines, including state of the art deep learning models, in precipitation nowcasting. Our results indicate that LHPF is competitive in various settings.

Gated Linear Networks

This paper presents a family of backpropagation-free neural architectures, Gated Linear Networks (GLNs),that are well suited to online learning applications where sample efficiency is of paramount importance. The impressive empirical performance of these architectures has long been known within the data compression community, but a theoretically satisfying explanation as to how and why they perform so well has proven difficult. What distinguishes these architectures from other neural systems is the distributed and local nature of their credit assignment mechanism; each neuron directly predicts the target and has its own set of hard-gated weights that are locally adapted via online convex optimization. By providing an interpretation, generalization and subsequent theoretical analysis, we show that sufficiently large GLNs are universal in a strong sense: not only can they model any compactly supported, continuous density function to arbitrary accuracy, but that any choice of no-regret online convex optimization technique will provably converge to the correct solution with enough data. Empirically we show a collection of single-pass learning results on established machine learning benchmarks that are competitive with results obtained with general purpose batch learning techniques.

Online Learning with Gated Linear Networks

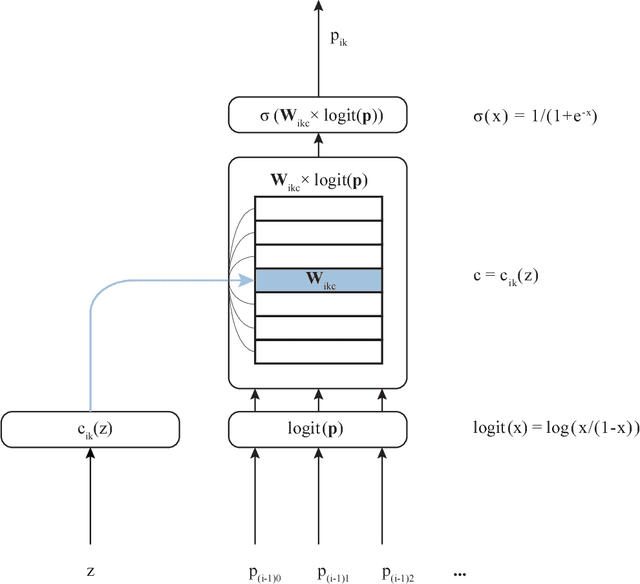
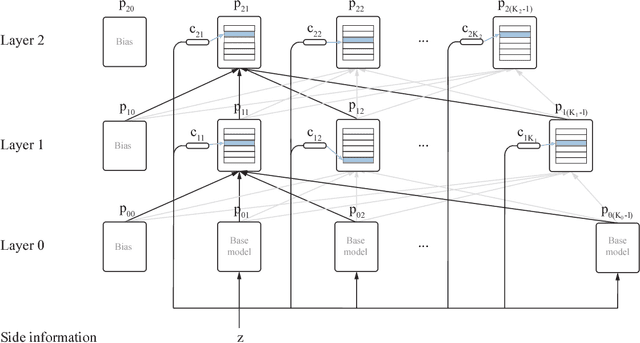
This paper describes a family of probabilistic architectures designed for online learning under the logarithmic loss. Rather than relying on non-linear transfer functions, our method gains representational power by the use of data conditioning. We state under general conditions a learnable capacity theorem that shows this approach can in principle learn any bounded Borel-measurable function on a compact subset of euclidean space; the result is stronger than many universality results for connectionist architectures because we provide both the model and the learning procedure for which convergence is guaranteed.