GENEOnet: Statistical analysis supporting explainability and trustworthiness

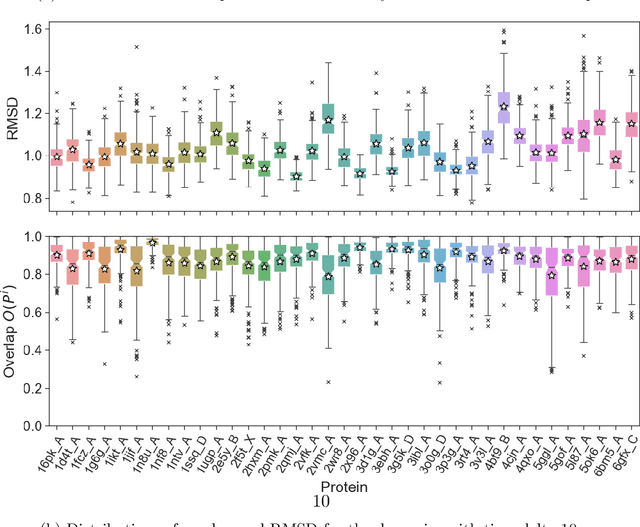
Group Equivariant Non-Expansive Operators (GENEOs) have emerged as mathematical tools for constructing networks for Machine Learning and Artificial Intelligence. Recent findings suggest that such models can be inserted within the domain of eXplainable Artificial Intelligence (XAI) due to their inherent interpretability. In this study, we aim to verify this claim with respect to GENEOnet, a GENEO network developed for an application in computational biochemistry by employing various statistical analyses and experiments. Such experiments first allow us to perform a sensitivity analysis on GENEOnet's parameters to test their significance. Subsequently, we show that GENEOnet exhibits a significantly higher proportion of equivariance compared to other methods. Lastly, we demonstrate that GENEOnet is on average robust to perturbations arising from molecular dynamics. These results collectively serve as proof of the explainability, trustworthiness, and robustness of GENEOnet and confirm the beneficial use of GENEOs in the context of Trustworthy Artificial Intelligence.

Mathematical Foundation of Interpretable Equivariant Surrogate Models

This paper introduces a rigorous mathematical framework for neural network explainability, and more broadly for the explainability of equivariant operators called Group Equivariant Operators (GEOs) based on Group Equivariant Non-Expansive Operators (GENEOs) transformations. The central concept involves quantifying the distance between GEOs by measuring the non-commutativity of specific diagrams. Additionally, the paper proposes a definition of interpretability of GEOs according to a complexity measure that can be defined according to each user preferences. Moreover, we explore the formal properties of this framework and show how it can be applied in classical machine learning scenarios, like image classification with convolutional neural networks.

A novel approach to graph distinction through GENEOs and permutants

The theory of Group Equivariant Non-Expansive Operators (GENEOs) was initially developed in Topological Data Analysis for the geometric approximation of data observers, including their invariances and symmetries. This paper departs from that line of research and explores the use of GENEOs for distinguishing $r$-regular graphs up to isomorphisms. In doing so, we aim to test the capabilities and flexibility of these operators. Our experiments show that GENEOs offer a good compromise between efficiency and computational cost in comparing $r$-regular graphs, while their actions on data are easily interpretable. This supports the idea that GENEOs could be a general-purpose approach to discriminative problems in Machine Learning when some structural information about data and observers is explicitly given.

A topological model for partial equivariance in deep learning and data analysis

In this article, we propose a topological model to encode partial equivariance in neural networks. To this end, we introduce a class of operators, called P-GENEOs, that change data expressed by measurements, respecting the action of certain sets of transformations, in a non-expansive way. If the set of transformations acting is a group, then we obtain the so-called GENEOs. We then study the spaces of measurements, whose domains are subject to the action of certain self-maps, and the space of P-GENEOs between these spaces. We define pseudo-metrics on them and show some properties of the resulting spaces. In particular, we show how such spaces have convenient approximation and convexity properties.

Low-Resource White-Box Semantic Segmentation of Supporting Towers on 3D Point Clouds via Signature Shape Identification

Research in 3D semantic segmentation has been increasing performance metrics, like the IoU, by scaling model complexity and computational resources, leaving behind researchers and practitioners that (1) cannot access the necessary resources and (2) do need transparency on the model decision mechanisms. In this paper, we propose SCENE-Net, a low-resource white-box model for 3D point cloud semantic segmentation. SCENE-Net identifies signature shapes on the point cloud via group equivariant non-expansive operators (GENEOs), providing intrinsic geometric interpretability. Our training time on a laptop is 85~min, and our inference time is 20~ms. SCENE-Net has 11 trainable geometrical parameters and requires fewer data than black-box models. SCENE--Net offers robustness to noisy labeling and data imbalance and has comparable IoU to state-of-the-art methods. With this paper, we release a 40~000 Km labeled dataset of rural terrain point clouds and our code implementation.

Generalized Permutants and Graph GENEOs

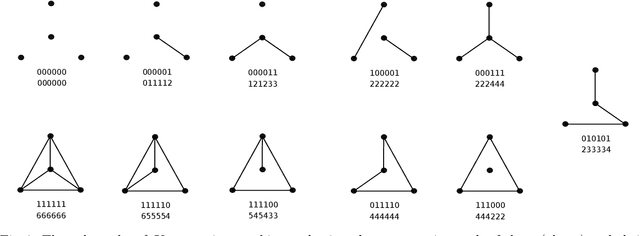
In this paper we establish a bridge between Topological Data Analysis and Geometric Deep Learning, adapting the topological theory of group equivariant non-expansive operators (GENEOs) to act on the space of all graphs weighted on vertices or edges. This is done by showing how the general concept of GENEO can be used to transform graphs and to give information about their structure. This requires the introduction of the new concepts of generalized permutant and generalized permutant measure and the mathematical proof that these concepts allow us to build GENEOs between graphs. An experimental section concludes the paper, illustrating the possible use of our operators to extract information from graphs. This paper is part of a line of research devoted to developing a compositional and geometric theory of GENEOs for Geometric Deep Learning.

GENEOnet: A new machine learning paradigm based on Group Equivariant Non-Expansive Operators. An application to protein pocket detection

Nowadays there is a big spotlight cast on the development of techniques of explainable machine learning. Here we introduce a new computational paradigm based on Group Equivariant Non-Expansive Operators, that can be regarded as the product of a rising mathematical theory of information-processing observers. This approach, that can be adjusted to different situations, may have many advantages over other common tools, like Neural Networks, such as: knowledge injection and information engineering, selection of relevant features, small number of parameters and higher transparency. We chose to test our method, called GENEOnet, on a key problem in drug design: detecting pockets on the surface of proteins that can host ligands. Experimental results confirmed that our method works well even with a quite small training set, providing thus a great computational advantage, while the final comparison with other state-of-the-art methods shows that GENEOnet provides better or comparable results in terms of accuracy.

On the geometric and Riemannian structure of the spaces of group equivariant non-expansive operators

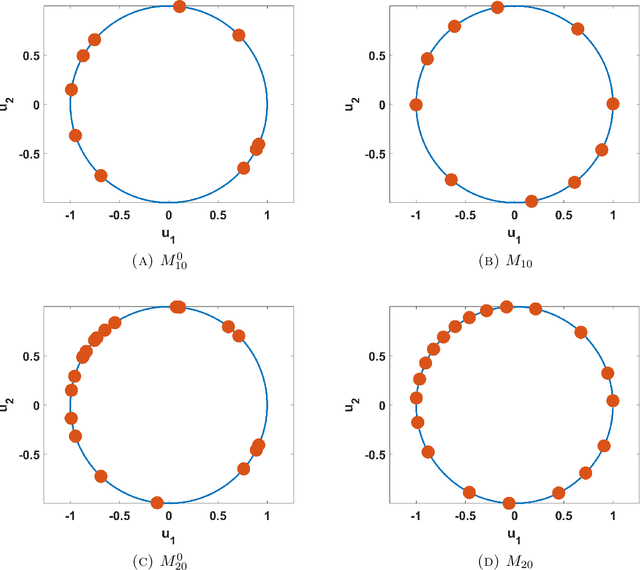
Group equivariant non-expansive operators have been recently proposed as basic components in topological data analysis and deep learning. In this paper we study some geometric properties of the spaces of group equivariant operators and show how a space $\mathcal{F}$ of group equivariant non-expansive operators can be endowed with the structure of a Riemannian manifold, so making available the use of gradient descent methods for the minimization of cost functions on $\mathcal{F}$. As an application of this approach, we also describe a procedure to select a finite set of representative group equivariant non-expansive operators in the considered manifold.

On the finite representation of group equivariant operators via permutant measures

The study of $G$-equivariant operators is of great interest to explain and understand the architecture of neural networks. In this paper we show that each linear $G$-equivariant operator can be produced by a suitable permutant measure, provided that the group $G$ transitively acts on a finite signal domain $X$. This result makes available a new method to build linear $G$-equivariant operators in the finite setting.

Parametric machines: a fresh approach to architecture search

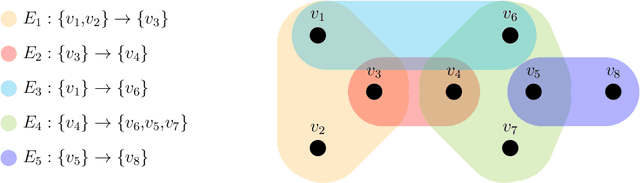
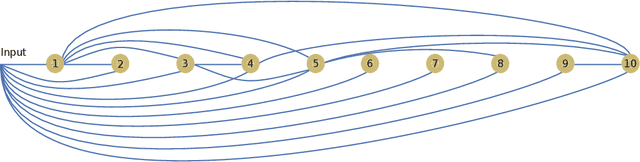
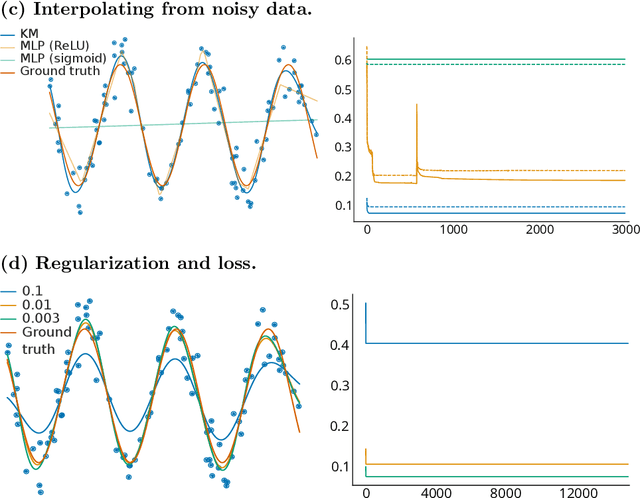
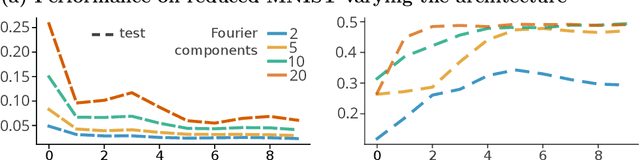
Using tools from category theory, we provide a framework where artificial neural networks, and their architectures, can be formally described. We first define the notion of machine in a general categorical context, and show how simple machines can be combined into more complex ones. We explore finite- and infinite-depth machines, which generalize neural networks and neural ordinary differential equations. Borrowing ideas from functional analysis and kernel methods, we build complete, normed, infinite-dimensional spaces of machines, and discuss how to find optimal architectures and parameters -- within those spaces -- to solve a given computational problem. In our numerical experiments, these kernel-inspired networks can outperform classical neural networks when the training dataset is small.