Persistence-based operators in machine learning

Artificial neural networks can learn complex, salient data features to achieve a given task. On the opposite end of the spectrum, mathematically grounded methods such as topological data analysis allow users to design analysis pipelines fully aware of data constraints and symmetries. We introduce a class of persistence-based neural network layers. Persistence-based layers allow the users to easily inject knowledge about symmetries (equivariance) respected by the data, are equipped with learnable weights, and can be composed with state-of-the-art neural architectures.

Neural network layers as parametric spans

Properties such as composability and automatic differentiation made artificial neural networks a pervasive tool in applications. Tackling more challenging problems caused neural networks to progressively become more complex and thus difficult to define from a mathematical perspective. We present a general definition of linear layer arising from a categorical framework based on the notions of integration theory and parametric spans. This definition generalizes and encompasses classical layers (e.g., dense, convolutional), while guaranteeing existence and computability of the layer's derivatives for backpropagation.

Machines of finite depth: towards a formalization of neural networks

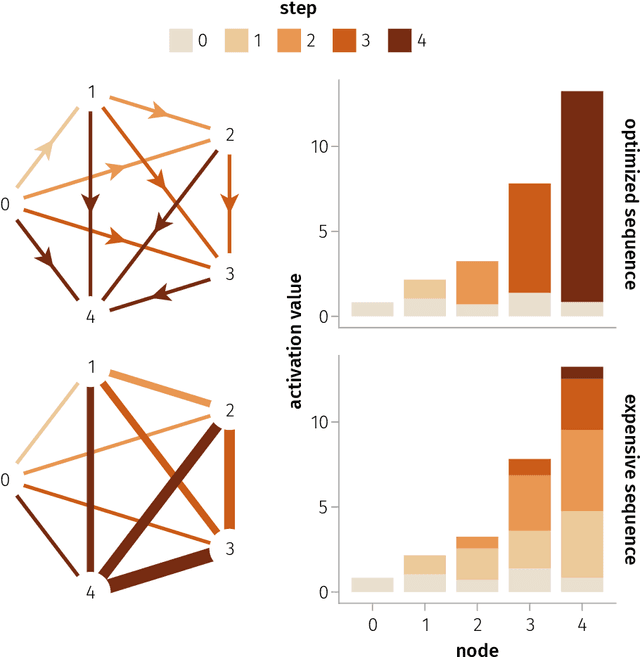
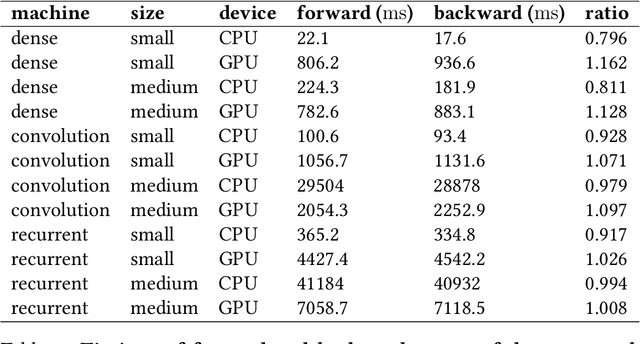
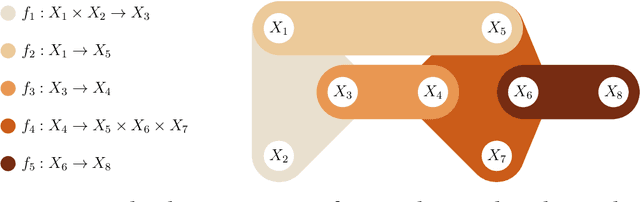
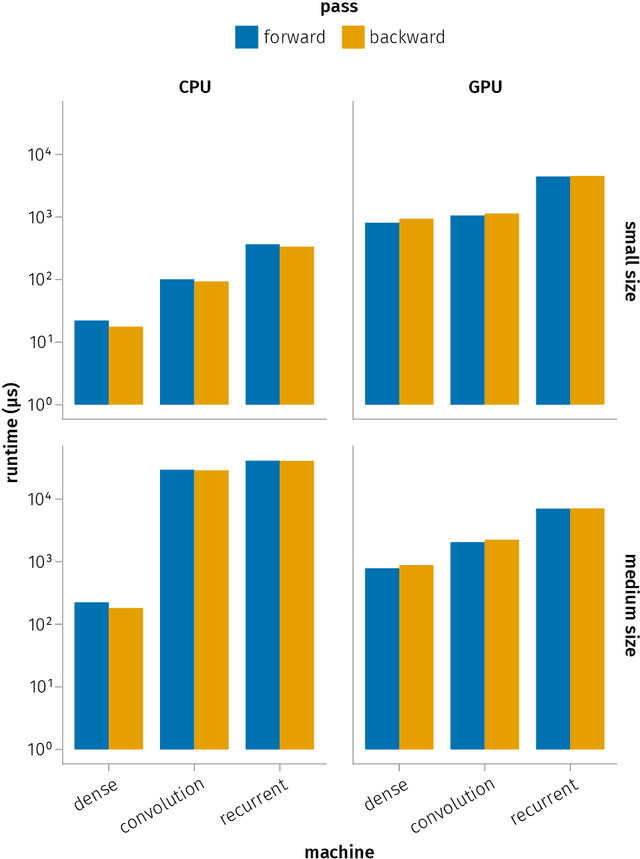
We provide a unifying framework where artificial neural networks and their architectures can be formally described as particular cases of a general mathematical construction--machines of finite depth. Unlike neural networks, machines have a precise definition, from which several properties follow naturally. Machines of finite depth are modular (they can be combined), efficiently computable and differentiable. The backward pass of a machine is again a machine and can be computed without overhead using the same procedure as the forward pass. We prove this statement theoretically and practically, via a unified implementation that generalizes several classical architectures--dense, convolutional, and recurrent neural networks with a rich shortcut structure--and their respective backpropagation rules.

Parametric machines: a fresh approach to architecture search

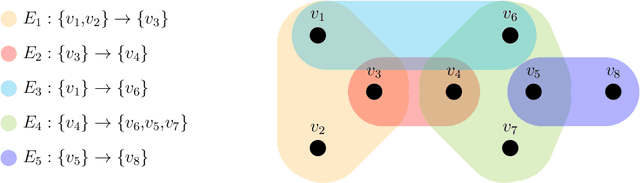
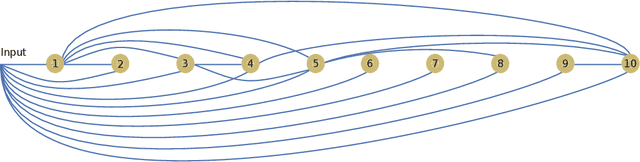
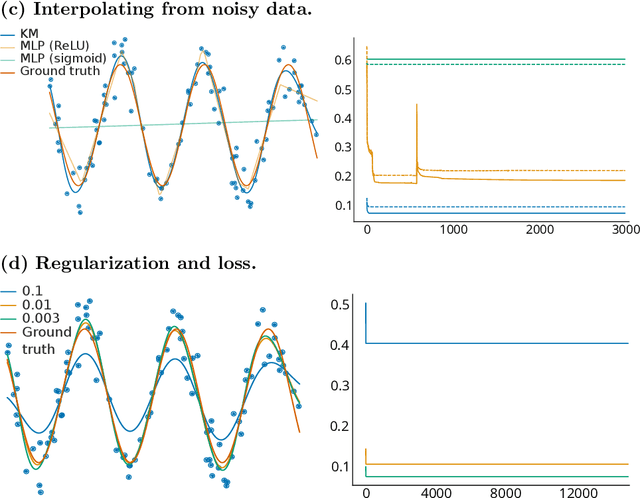
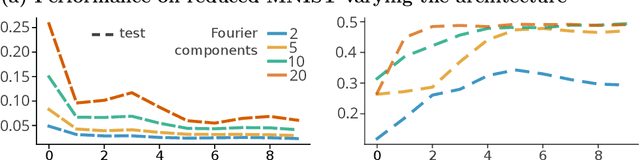
Using tools from category theory, we provide a framework where artificial neural networks, and their architectures, can be formally described. We first define the notion of machine in a general categorical context, and show how simple machines can be combined into more complex ones. We explore finite- and infinite-depth machines, which generalize neural networks and neural ordinary differential equations. Borrowing ideas from functional analysis and kernel methods, we build complete, normed, infinite-dimensional spaces of machines, and discuss how to find optimal architectures and parameters -- within those spaces -- to solve a given computational problem. In our numerical experiments, these kernel-inspired networks can outperform classical neural networks when the training dataset is small.

Towards a topological-geometrical theory of group equivariant non-expansive operators for data analysis and machine learning

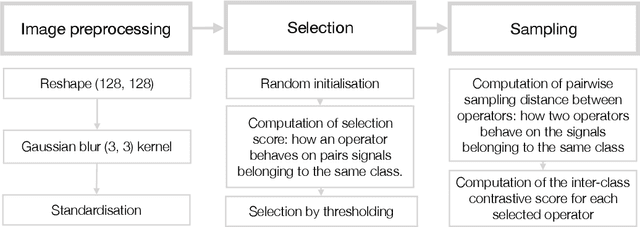
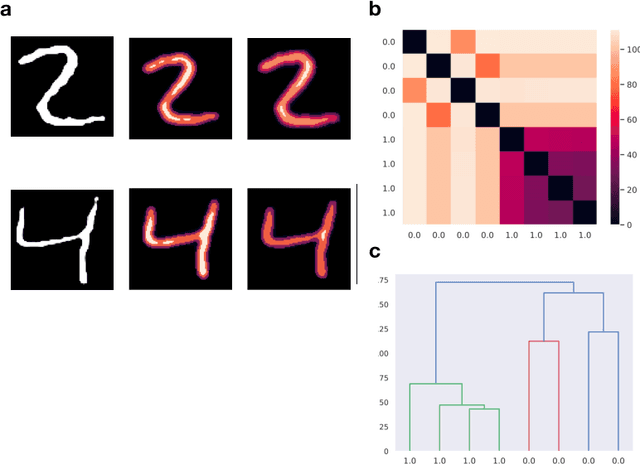
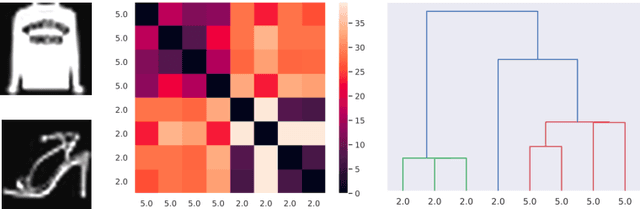
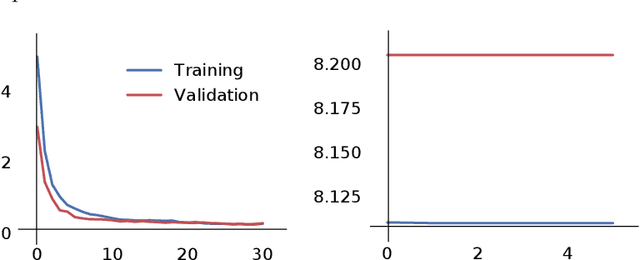
The aim of this paper is to provide a general mathematical framework for group equivariance in the machine learning context. The framework builds on a synergy between persistent homology and the theory of group actions. We define group-equivariant non-expansive operators (GENEOs), which are maps between function spaces associated with groups of transformations. We study the topological and metric properties of the space of GENEOs to evaluate their approximating power and set the basis for general strategies to initialise and compose operators. We begin by defining suitable pseudo-metrics for the function spaces, the equivariance groups, and the set of non-expansive operators. Basing on these pseudo-metrics, we prove that the space of GENEOs is compact and convex, under the assumption that the function spaces are compact and convex. These results provide fundamental guarantees in a machine learning perspective. We show examples on the MNIST and fashion-MNIST datasets. By considering isometry-equivariant non-expansive operators, we describe a simple strategy to select and sample operators, and show how the selected and sampled operators can be used to perform both classical metric learning and an effective initialisation of the kernels of a convolutional neural network.

idtracker.ai: Tracking all individuals in large collectives of unmarked animals

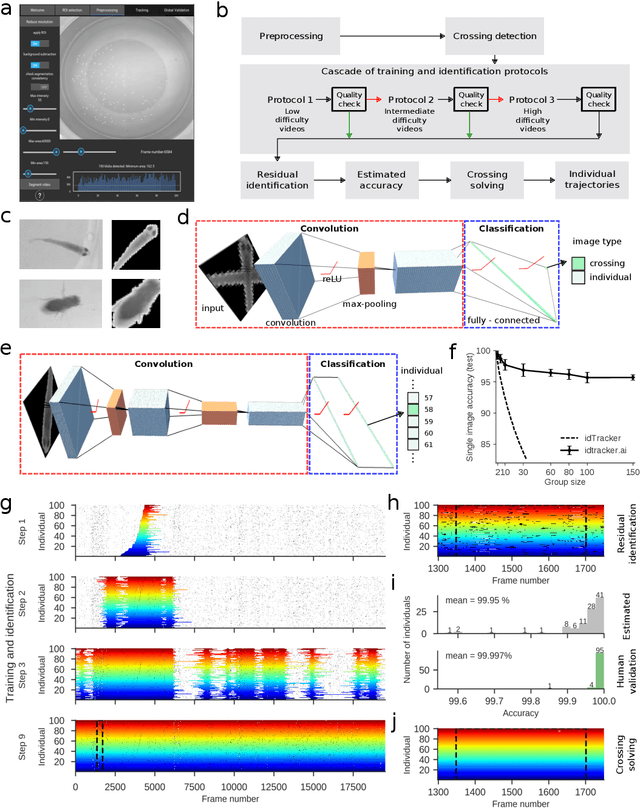
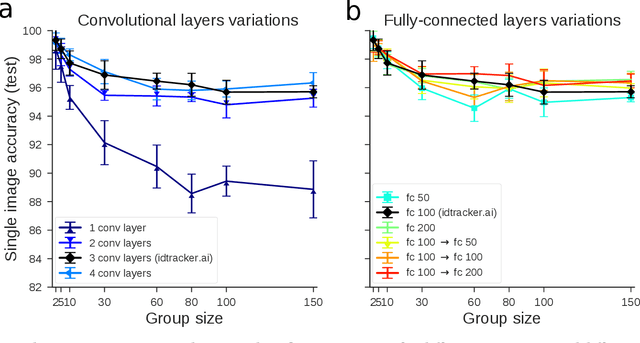
Our understanding of collective animal behavior is limited by our ability to track each of the individuals. We describe an algorithm and software, idtracker.ai, that extracts from video all trajectories with correct identities at a high accuracy for collectives of up to 100 individuals. It uses two deep networks, one detecting when animals touch or cross and another one for animal identification, trained adaptively to conditions and difficulty of the video.