Algebraic Machine Learning: Learning as computing an algebraic decomposition of a task

Statistics and Optimization are foundational to modern Machine Learning. Here, we propose an alternative foundation based on Abstract Algebra, with mathematics that facilitates the analysis of learning. In this approach, the goal of the task and the data are encoded as axioms of an algebra, and a model is obtained where only these axioms and their logical consequences hold. Although this is not a generalizing model, we show that selecting specific subsets of its breakdown into algebraic atoms obtained via subdirect decomposition gives a model that generalizes. We validate this new learning principle on standard datasets such as MNIST, FashionMNIST, CIFAR-10, and medical images, achieving performance comparable to optimized multilayer perceptrons. Beyond data-driven tasks, the new learning principle extends to formal problems, such as finding Hamiltonian cycles from their specifications and without relying on search. This algebraic foundation offers a fresh perspective on machine intelligence, featuring direct learning from training data without the need for validation dataset, scaling through model additivity, and asymptotic convergence to the underlying rule in the data.

Supervised dimensionality reduction by a Linear Discriminant Analysis on pre-trained CNN features

We explore the application of linear discriminant analysis (LDA) to the features obtained in different layers of pretrained deep convolutional neural networks (CNNs). The advantage of LDA compared to other techniques in dimensionality reduction is that it reduces dimensions while preserving the global structure of data, so distances in the low-dimensional structure found are meaningful. The LDA applied to the CNN features finds that the centroids of classes corresponding to the similar data lay closer than classes corresponding to different data. We applied the method to a modification of the MNIST dataset with ten additional classes, each new class with half of the images from one of the standard ten classes. The method finds the new classes close to the corresponding standard classes we took the data form. We also applied the method to a dataset of images of butterflies to find that related subspecies are found to be close. For both datasets, we find a performance similar to state-of-the-art methods.

Algebraic Machine Learning

Machine learning algorithms use error function minimization to fit a large set of parameters in a preexisting model. However, error minimization eventually leads to a memorization of the training dataset, losing the ability to generalize to other datasets. To achieve generalization something else is needed, for example a regularization method or stopping the training when error in a validation dataset is minimal. Here we propose a different approach to learning and generalization that is parameter-free, fully discrete and that does not use function minimization. We use the training data to find an algebraic representation with minimal size and maximal freedom, explicitly expressed as a product of irreducible components. This algebraic representation is shown to directly generalize, giving high accuracy in test data, more so the smaller the representation. We prove that the number of generalizing representations can be very large and the algebra only needs to find one. We also derive and test a relationship between compression and error rate. We give results for a simple problem solved step by step, hand-written character recognition, and the Queens Completion problem as an example of unsupervised learning. As an alternative to statistical learning, algebraic learning may offer advantages in combining bottom-up and top-down information, formal concept derivation from data and large-scale parallelization.

idtracker.ai: Tracking all individuals in large collectives of unmarked animals

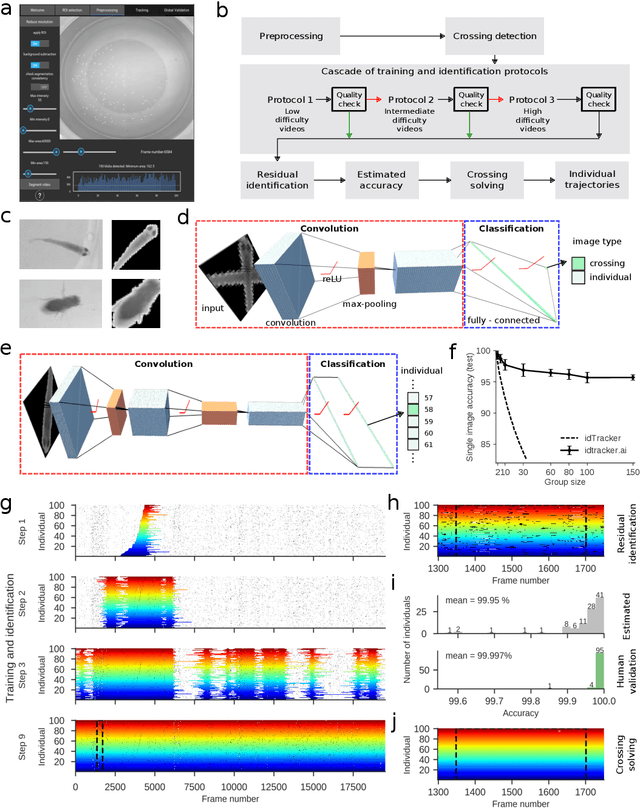
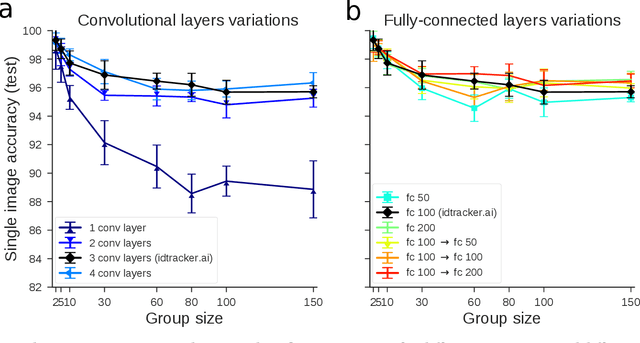
Our understanding of collective animal behavior is limited by our ability to track each of the individuals. We describe an algorithm and software, idtracker.ai, that extracts from video all trajectories with correct identities at a high accuracy for collectives of up to 100 individuals. It uses two deep networks, one detecting when animals touch or cross and another one for animal identification, trained adaptively to conditions and difficulty of the video.