Machines of finite depth: towards a formalization of neural networks
Paper and Code
Apr 27, 2022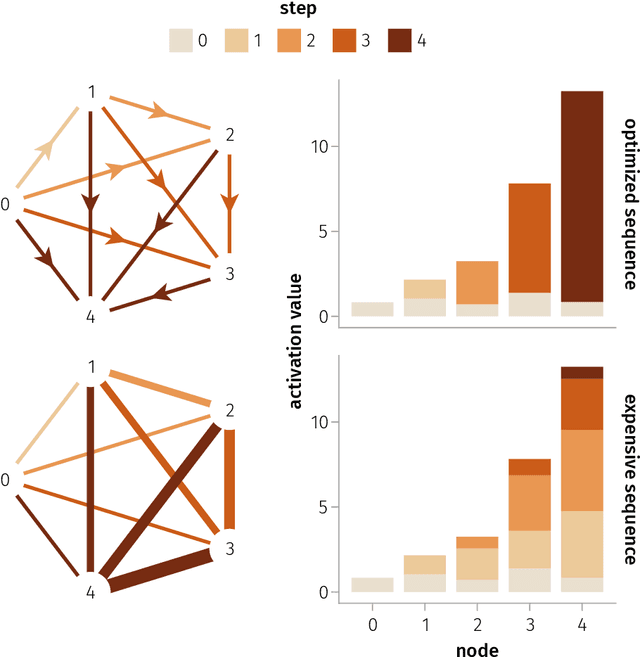
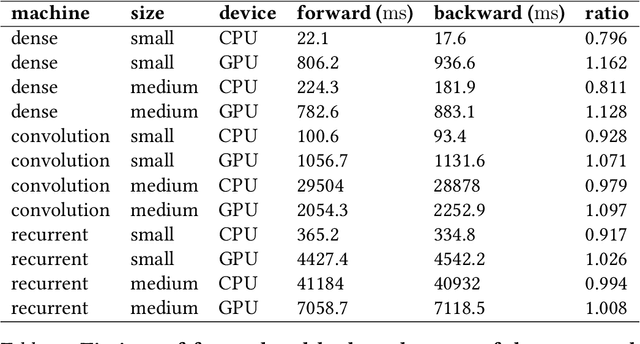
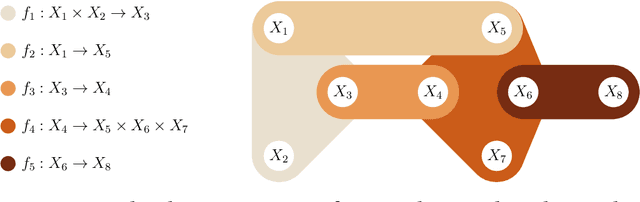
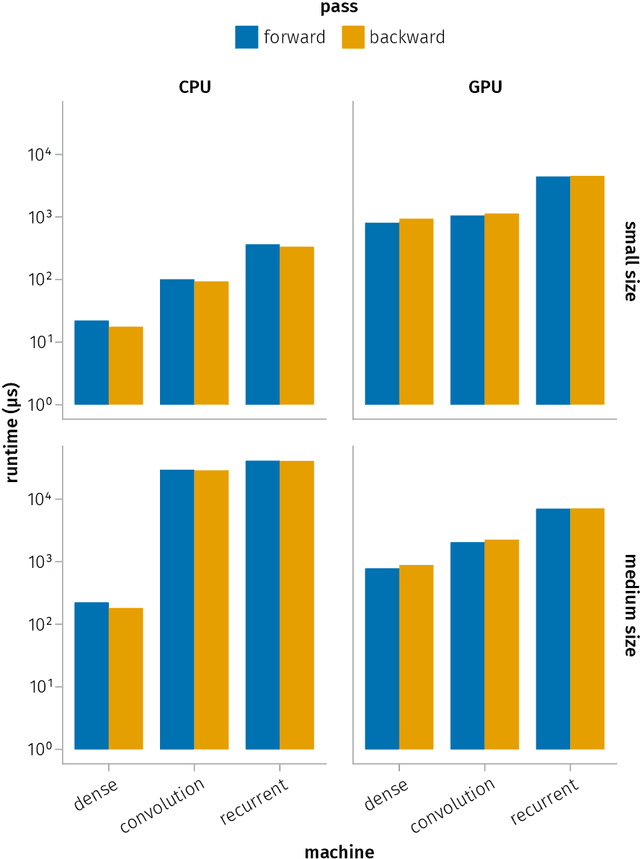
We provide a unifying framework where artificial neural networks and their architectures can be formally described as particular cases of a general mathematical construction--machines of finite depth. Unlike neural networks, machines have a precise definition, from which several properties follow naturally. Machines of finite depth are modular (they can be combined), efficiently computable and differentiable. The backward pass of a machine is again a machine and can be computed without overhead using the same procedure as the forward pass. We prove this statement theoretically and practically, via a unified implementation that generalizes several classical architectures--dense, convolutional, and recurrent neural networks with a rich shortcut structure--and their respective backpropagation rules.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge