A novel approach to graph distinction through GENEOs and permutants

The theory of Group Equivariant Non-Expansive Operators (GENEOs) was initially developed in Topological Data Analysis for the geometric approximation of data observers, including their invariances and symmetries. This paper departs from that line of research and explores the use of GENEOs for distinguishing $r$-regular graphs up to isomorphisms. In doing so, we aim to test the capabilities and flexibility of these operators. Our experiments show that GENEOs offer a good compromise between efficiency and computational cost in comparing $r$-regular graphs, while their actions on data are easily interpretable. This supports the idea that GENEOs could be a general-purpose approach to discriminative problems in Machine Learning when some structural information about data and observers is explicitly given.

Persistence-based operators in machine learning

Artificial neural networks can learn complex, salient data features to achieve a given task. On the opposite end of the spectrum, mathematically grounded methods such as topological data analysis allow users to design analysis pipelines fully aware of data constraints and symmetries. We introduce a class of persistence-based neural network layers. Persistence-based layers allow the users to easily inject knowledge about symmetries (equivariance) respected by the data, are equipped with learnable weights, and can be composed with state-of-the-art neural architectures.

Generalized Permutants and Graph GENEOs

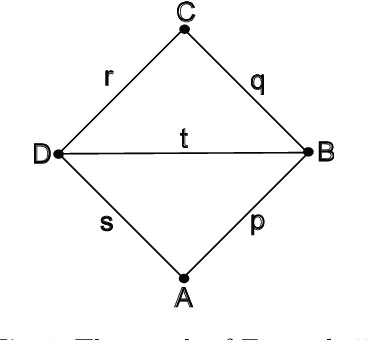
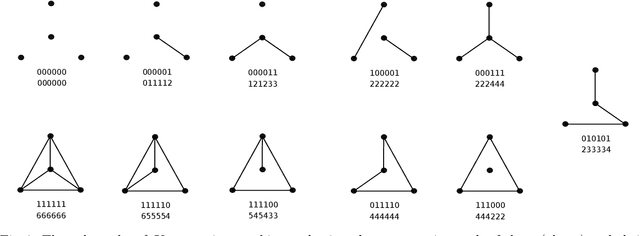
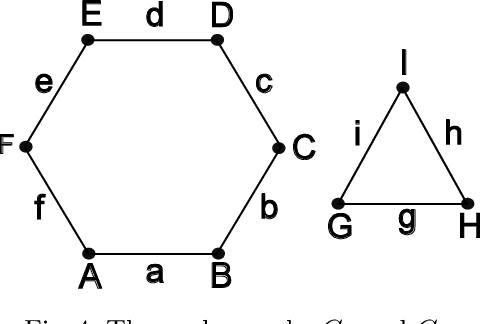
In this paper we establish a bridge between Topological Data Analysis and Geometric Deep Learning, adapting the topological theory of group equivariant non-expansive operators (GENEOs) to act on the space of all graphs weighted on vertices or edges. This is done by showing how the general concept of GENEO can be used to transform graphs and to give information about their structure. This requires the introduction of the new concepts of generalized permutant and generalized permutant measure and the mathematical proof that these concepts allow us to build GENEOs between graphs. An experimental section concludes the paper, illustrating the possible use of our operators to extract information from graphs. This paper is part of a line of research devoted to developing a compositional and geometric theory of GENEOs for Geometric Deep Learning.

Comparing persistence diagrams through complex vectors

The natural pseudo-distance of spaces endowed with filtering functions is precious for shape classification and retrieval; its optimal estimate coming from persistence diagrams is the bottleneck distance, which unfortunately suffers from combinatorial explosion. A possible algebraic representation of persistence diagrams is offered by complex polynomials; since far polynomials represent far persistence diagrams, a fast comparison of the coefficient vectors can reduce the size of the database to be classified by the bottleneck distance. This article explores experimentally three transformations from diagrams to polynomials and three distances between the complex vectors of coefficients.