Faraz Ahmad
Generalized Permutants and Graph GENEOs
Jun 29, 2022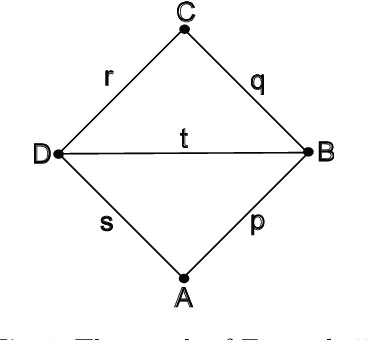

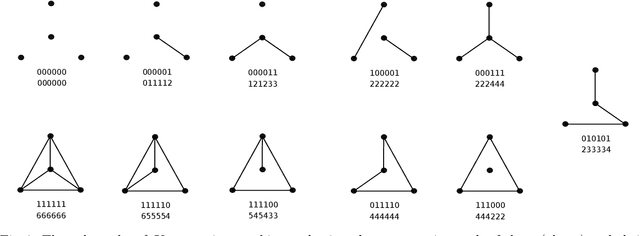
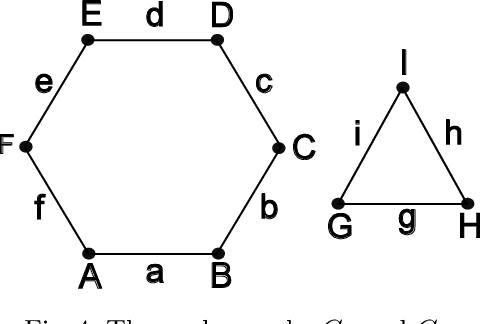
Abstract:In this paper we establish a bridge between Topological Data Analysis and Geometric Deep Learning, adapting the topological theory of group equivariant non-expansive operators (GENEOs) to act on the space of all graphs weighted on vertices or edges. This is done by showing how the general concept of GENEO can be used to transform graphs and to give information about their structure. This requires the introduction of the new concepts of generalized permutant and generalized permutant measure and the mathematical proof that these concepts allow us to build GENEOs between graphs. An experimental section concludes the paper, illustrating the possible use of our operators to extract information from graphs. This paper is part of a line of research devoted to developing a compositional and geometric theory of GENEOs for Geometric Deep Learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge