Towards a topological-geometrical theory of group equivariant non-expansive operators for data analysis and machine learning
Paper and Code
Dec 31, 2018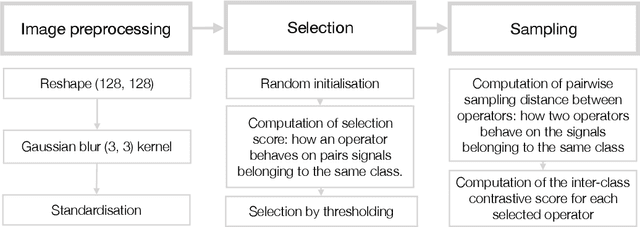
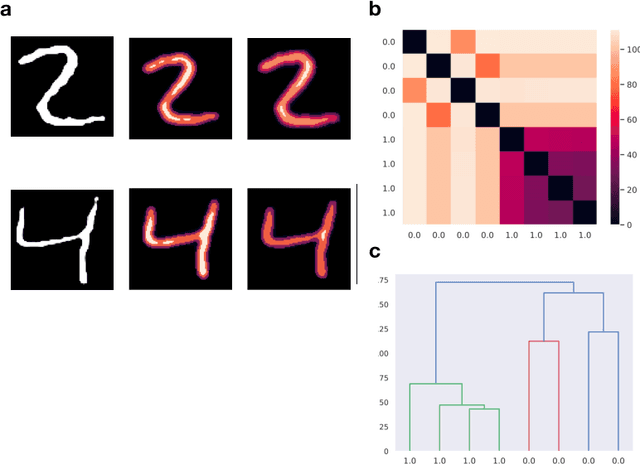
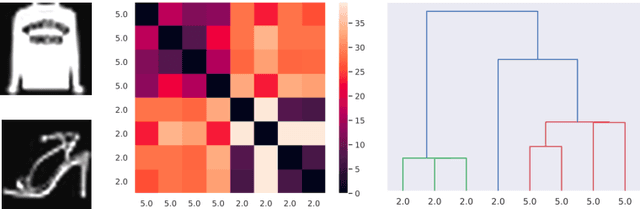
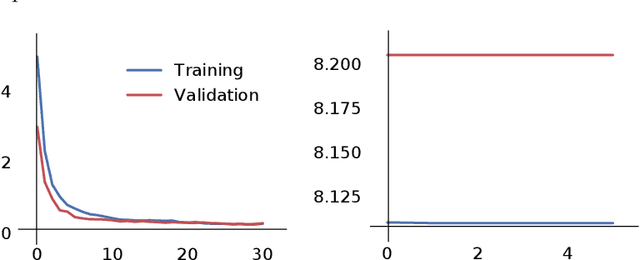
The aim of this paper is to provide a general mathematical framework for group equivariance in the machine learning context. The framework builds on a synergy between persistent homology and the theory of group actions. We define group-equivariant non-expansive operators (GENEOs), which are maps between function spaces associated with groups of transformations. We study the topological and metric properties of the space of GENEOs to evaluate their approximating power and set the basis for general strategies to initialise and compose operators. We begin by defining suitable pseudo-metrics for the function spaces, the equivariance groups, and the set of non-expansive operators. Basing on these pseudo-metrics, we prove that the space of GENEOs is compact and convex, under the assumption that the function spaces are compact and convex. These results provide fundamental guarantees in a machine learning perspective. We show examples on the MNIST and fashion-MNIST datasets. By considering isometry-equivariant non-expansive operators, we describe a simple strategy to select and sample operators, and show how the selected and sampled operators can be used to perform both classical metric learning and an effective initialisation of the kernels of a convolutional neural network.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge