An Algebraic Representation Theorem for Linear GENEOs in Geometric Machine Learning

Geometric and Topological Deep Learning are rapidly growing research areas that enhance machine learning through the use of geometric and topological structures. Within this framework, Group Equivariant Non-Expansive Operators (GENEOs) have emerged as a powerful class of operators for encoding symmetries and designing efficient, interpretable neural architectures. Originally introduced in Topological Data Analysis, GENEOs have since found applications in Deep Learning as tools for constructing equivariant models with reduced parameter complexity. GENEOs provide a unifying framework bridging Geometric and Topological Deep Learning and include the operator computing persistence diagrams as a special case. Their theoretical foundations rely on group actions, equivariance, and compactness properties of operator spaces, grounding them in algebra and geometry while enabling both mathematical rigor and practical relevance. While a previous representation theorem characterized linear GENEOs acting on data of the same type, many real-world applications require operators between heterogeneous data spaces. In this work, we address this limitation by introducing a new representation theorem for linear GENEOs acting between different perception pairs, based on generalized T-permutant measures. Under mild assumptions on the data domains and group actions, our result provides a complete characterization of such operators. We also prove the compactness and convexity of the space of linear GENEOs. We further demonstrate the practical impact of this theory by applying the proposed framework to improve the performance of autoencoders, highlighting the relevance of GENEOs in modern machine learning applications.

A topological model for partial equivariance in deep learning and data analysis

In this article, we propose a topological model to encode partial equivariance in neural networks. To this end, we introduce a class of operators, called P-GENEOs, that change data expressed by measurements, respecting the action of certain sets of transformations, in a non-expansive way. If the set of transformations acting is a group, then we obtain the so-called GENEOs. We then study the spaces of measurements, whose domains are subject to the action of certain self-maps, and the space of P-GENEOs between these spaces. We define pseudo-metrics on them and show some properties of the resulting spaces. In particular, we show how such spaces have convenient approximation and convexity properties.

On the geometric and Riemannian structure of the spaces of group equivariant non-expansive operators

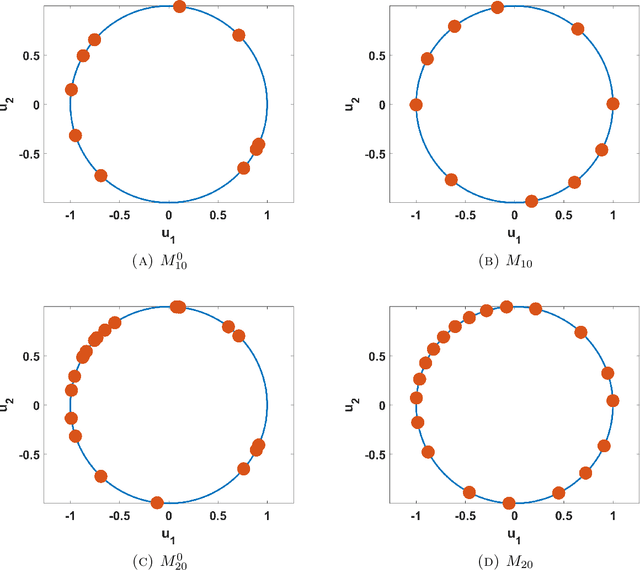
Group equivariant non-expansive operators have been recently proposed as basic components in topological data analysis and deep learning. In this paper we study some geometric properties of the spaces of group equivariant operators and show how a space $\mathcal{F}$ of group equivariant non-expansive operators can be endowed with the structure of a Riemannian manifold, so making available the use of gradient descent methods for the minimization of cost functions on $\mathcal{F}$. As an application of this approach, we also describe a procedure to select a finite set of representative group equivariant non-expansive operators in the considered manifold.

On the finite representation of group equivariant operators via permutant measures

The study of $G$-equivariant operators is of great interest to explain and understand the architecture of neural networks. In this paper we show that each linear $G$-equivariant operator can be produced by a suitable permutant measure, provided that the group $G$ transitively acts on a finite signal domain $X$. This result makes available a new method to build linear $G$-equivariant operators in the finite setting.

Towards a topological-geometrical theory of group equivariant non-expansive operators for data analysis and machine learning

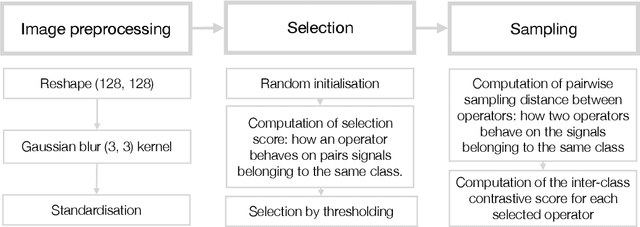
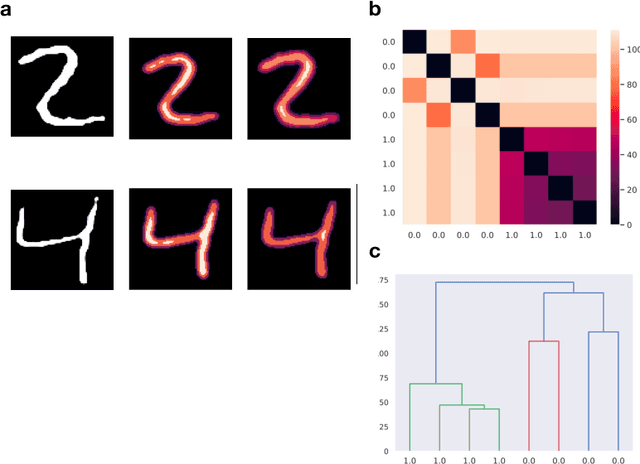
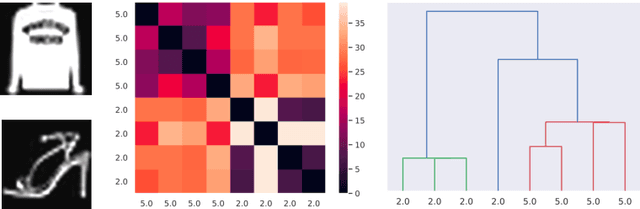
The aim of this paper is to provide a general mathematical framework for group equivariance in the machine learning context. The framework builds on a synergy between persistent homology and the theory of group actions. We define group-equivariant non-expansive operators (GENEOs), which are maps between function spaces associated with groups of transformations. We study the topological and metric properties of the space of GENEOs to evaluate their approximating power and set the basis for general strategies to initialise and compose operators. We begin by defining suitable pseudo-metrics for the function spaces, the equivariance groups, and the set of non-expansive operators. Basing on these pseudo-metrics, we prove that the space of GENEOs is compact and convex, under the assumption that the function spaces are compact and convex. These results provide fundamental guarantees in a machine learning perspective. We show examples on the MNIST and fashion-MNIST datasets. By considering isometry-equivariant non-expansive operators, we describe a simple strategy to select and sample operators, and show how the selected and sampled operators can be used to perform both classical metric learning and an effective initialisation of the kernels of a convolutional neural network.