Naiyang Guan
MVP: Meta Visual Prompt Tuning for Few-Shot Remote Sensing Image Scene Classification
Sep 17, 2023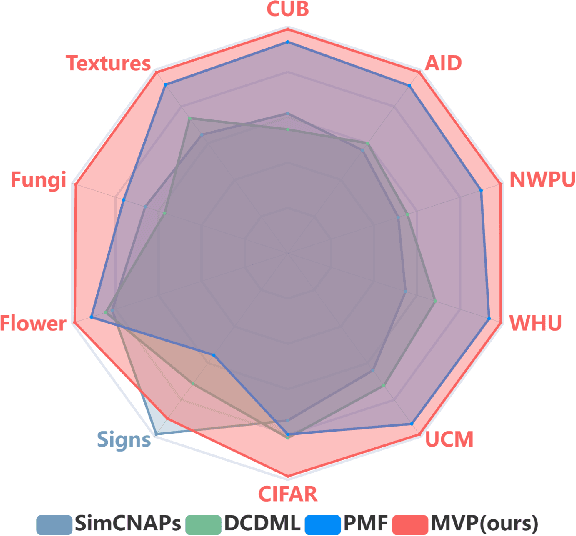
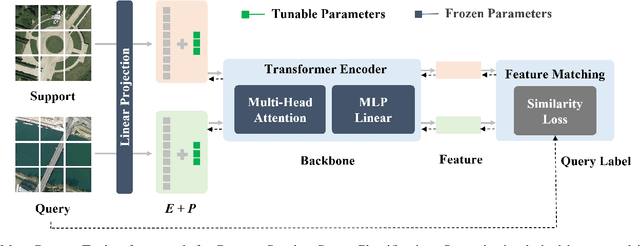
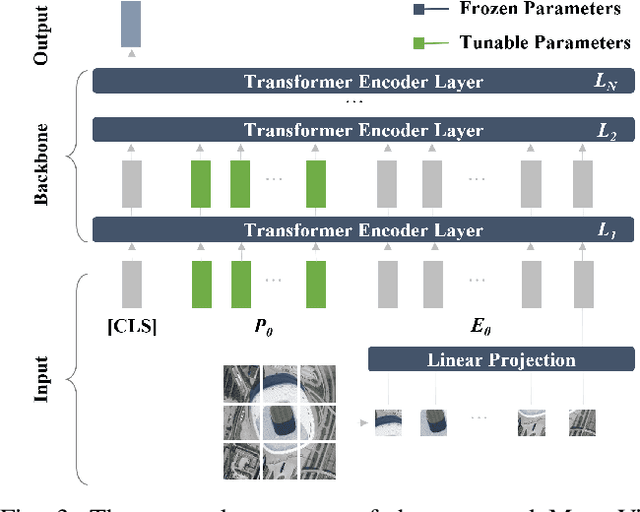
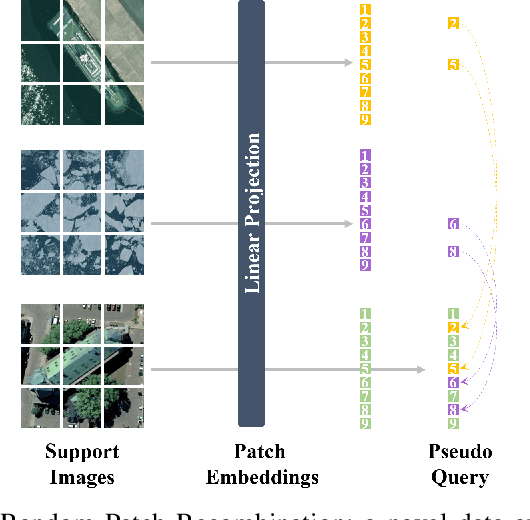
Abstract:Vision Transformer (ViT) models have recently emerged as powerful and versatile models for various visual tasks. Recently, a work called PMF has achieved promising results in few-shot image classification by utilizing pre-trained vision transformer models. However, PMF employs full fine-tuning for learning the downstream tasks, leading to significant overfitting and storage issues, especially in the remote sensing domain. In order to tackle these issues, we turn to the recently proposed parameter-efficient tuning methods, such as VPT, which updates only the newly added prompt parameters while keeping the pre-trained backbone frozen. Inspired by VPT, we propose the Meta Visual Prompt Tuning (MVP) method. Specifically, we integrate the VPT method into the meta-learning framework and tailor it to the remote sensing domain, resulting in an efficient framework for Few-Shot Remote Sensing Scene Classification (FS-RSSC). Furthermore, we introduce a novel data augmentation strategy based on patch embedding recombination to enhance the representation and diversity of scenes for classification purposes. Experiment results on the FS-RSSC benchmark demonstrate the superior performance of the proposed MVP over existing methods in various settings, such as various-way-various-shot, various-way-one-shot, and cross-domain adaptation.
PVP: Pre-trained Visual Parameter-Efficient Tuning
Apr 26, 2023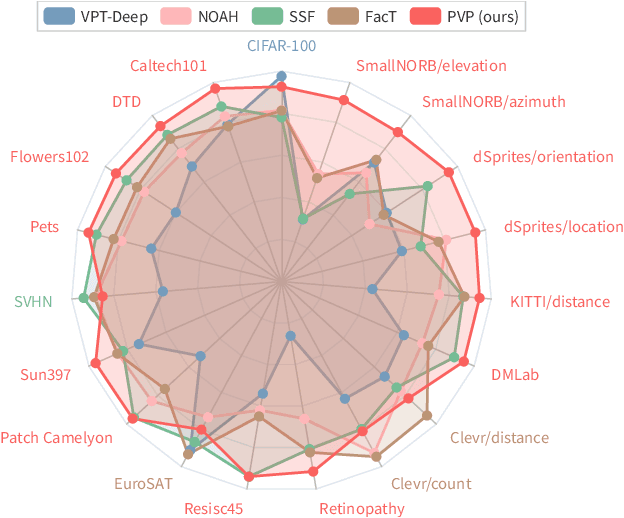
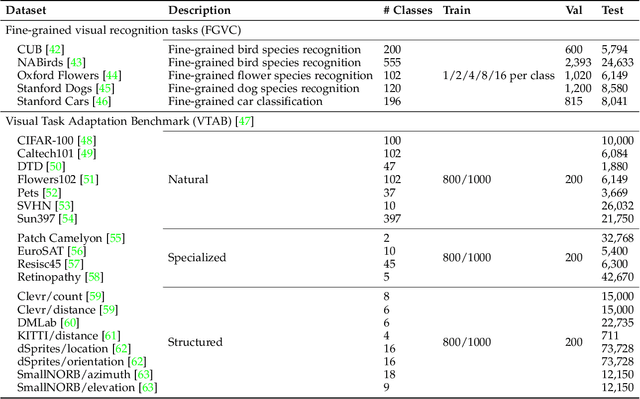
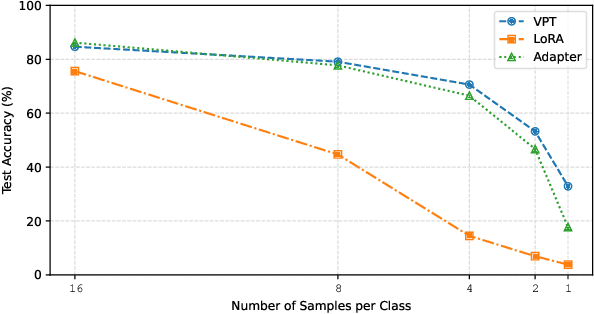
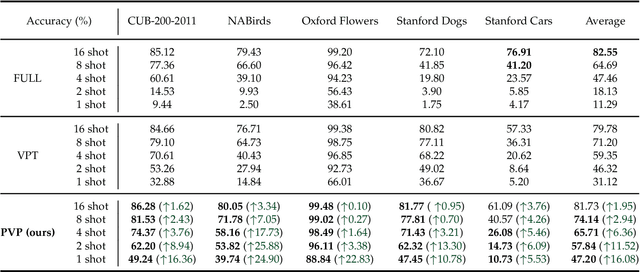
Abstract:Large-scale pre-trained transformers have demonstrated remarkable success in various computer vision tasks. However, it is still highly challenging to fully fine-tune these models for downstream tasks due to their high computational and storage costs. Recently, Parameter-Efficient Tuning (PETuning) techniques, e.g., Visual Prompt Tuning (VPT) and Low-Rank Adaptation (LoRA), have significantly reduced the computation and storage cost by inserting lightweight prompt modules into the pre-trained models and tuning these prompt modules with a small number of trainable parameters, while keeping the transformer backbone frozen. Although only a few parameters need to be adjusted, most PETuning methods still require a significant amount of downstream task training data to achieve good results. The performance is inadequate on low-data regimes, especially when there are only one or two examples per class. To this end, we first empirically identify the poor performance is mainly due to the inappropriate way of initializing prompt modules, which has also been verified in the pre-trained language models. Next, we propose a Pre-trained Visual Parameter-efficient (PVP) Tuning framework, which pre-trains the parameter-efficient tuning modules first and then leverages the pre-trained modules along with the pre-trained transformer backbone to perform parameter-efficient tuning on downstream tasks. Experiment results on five Fine-Grained Visual Classification (FGVC) and VTAB-1k datasets demonstrate that our proposed method significantly outperforms state-of-the-art PETuning methods.
Truncated Cauchy Non-negative Matrix Factorization
Jun 02, 2019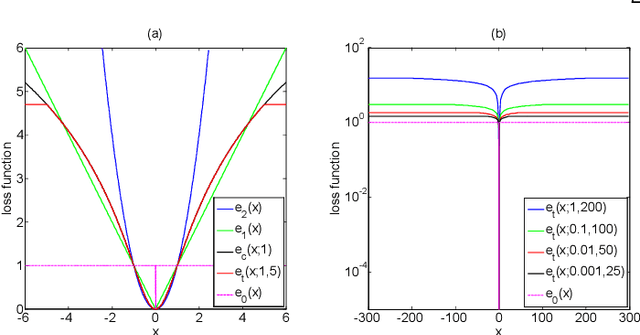



Abstract:Non-negative matrix factorization (NMF) minimizes the Euclidean distance between the data matrix and its low rank approximation, and it fails when applied to corrupted data because the loss function is sensitive to outliers. In this paper, we propose a Truncated CauchyNMF loss that handle outliers by truncating large errors, and develop a Truncated CauchyNMF to robustly learn the subspace on noisy datasets contaminated by outliers. We theoretically analyze the robustness of Truncated CauchyNMF comparing with the competing models and theoretically prove that Truncated CauchyNMF has a generalization bound which converges at a rate of order $O(\sqrt{{\ln n}/{n}})$, where $n$ is the sample size. We evaluate Truncated CauchyNMF by image clustering on both simulated and real datasets. The experimental results on the datasets containing gross corruptions validate the effectiveness and robustness of Truncated CauchyNMF for learning robust subspaces.
MahNMF: Manhattan Non-negative Matrix Factorization
Jul 14, 2012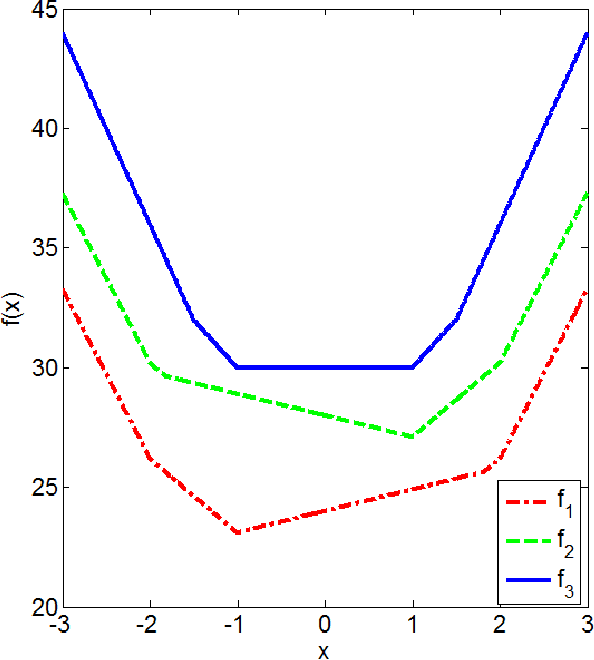
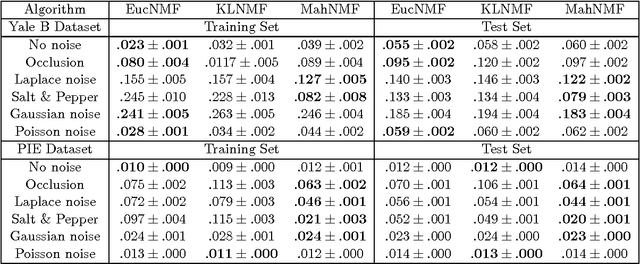
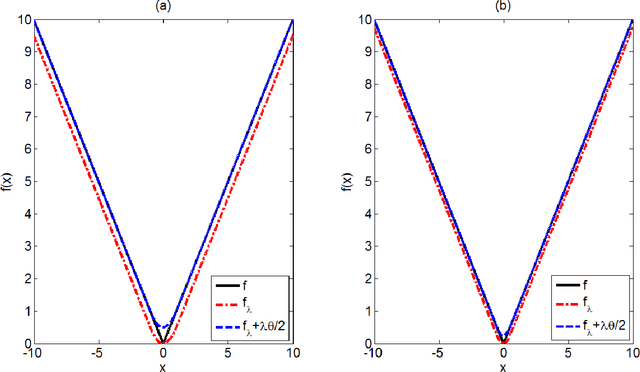
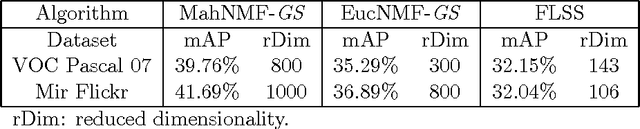
Abstract:Non-negative matrix factorization (NMF) approximates a non-negative matrix $X$ by a product of two non-negative low-rank factor matrices $W$ and $H$. NMF and its extensions minimize either the Kullback-Leibler divergence or the Euclidean distance between $X$ and $W^T H$ to model the Poisson noise or the Gaussian noise. In practice, when the noise distribution is heavy tailed, they cannot perform well. This paper presents Manhattan NMF (MahNMF) which minimizes the Manhattan distance between $X$ and $W^T H$ for modeling the heavy tailed Laplacian noise. Similar to sparse and low-rank matrix decompositions, MahNMF robustly estimates the low-rank part and the sparse part of a non-negative matrix and thus performs effectively when data are contaminated by outliers. We extend MahNMF for various practical applications by developing box-constrained MahNMF, manifold regularized MahNMF, group sparse MahNMF, elastic net inducing MahNMF, and symmetric MahNMF. The major contribution of this paper lies in two fast optimization algorithms for MahNMF and its extensions: the rank-one residual iteration (RRI) method and Nesterov's smoothing method. In particular, by approximating the residual matrix by the outer product of one row of W and one row of $H$ in MahNMF, we develop an RRI method to iteratively update each variable of $W$ and $H$ in a closed form solution. Although RRI is efficient for small scale MahNMF and some of its extensions, it is neither scalable to large scale matrices nor flexible enough to optimize all MahNMF extensions. Since the objective functions of MahNMF and its extensions are neither convex nor smooth, we apply Nesterov's smoothing method to recursively optimize one factor matrix with another matrix fixed. By setting the smoothing parameter inversely proportional to the iteration number, we improve the approximation accuracy iteratively for both MahNMF and its extensions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge