Distributed Speculative Inference of Large Language Models

Accelerating the inference of large language models (LLMs) is an important challenge in artificial intelligence. This paper introduces distributed speculative inference (DSI), a novel distributed inference algorithm that is provably faster than speculative inference (SI) [leviathan2023fast, chen2023accelerating, miao2023specinfer] and traditional autoregressive inference (non-SI). Like other SI algorithms, DSI works on frozen LLMs, requiring no training or architectural modifications, and it preserves the target distribution. Prior studies on SI have demonstrated empirical speedups (compared to non-SI) but require a fast and accurate drafter LLM. In practice, off-the-shelf LLMs often do not have matching drafters that are sufficiently fast and accurate. We show a gap: SI gets slower than non-SI when using slower or less accurate drafters. We close this gap by proving that DSI is faster than both SI and non-SI given any drafters. By orchestrating multiple instances of the target and drafters, DSI is not only faster than SI but also supports LLMs that cannot be accelerated with SI. Our simulations show speedups of off-the-shelf LLMs in realistic settings: DSI is 1.29-1.92x faster than SI.

Accelerating Speculative Decoding using Dynamic Speculation Length

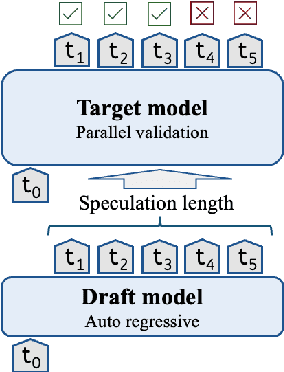
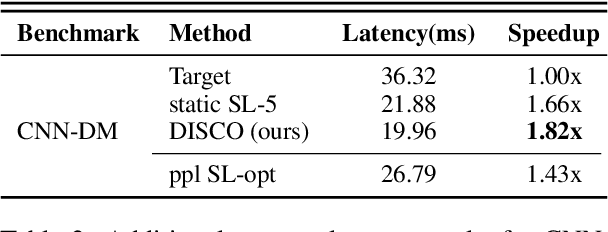
Speculative decoding is a promising method for reducing the inference latency of large language models. The effectiveness of the method depends on the speculation length (SL) - the number of tokens generated by the draft model at each iteration. The vast majority of speculative decoding approaches use the same SL for all iterations. In this work, we show that this practice is suboptimal. We introduce DISCO, a DynamIc SpeCulation length Optimization method that uses a classifier to dynamically adjust the SL at each iteration, while provably preserving the decoding quality. Experiments with four benchmarks demonstrate average speedup gains of 10.3% relative to our best baselines.

StarCoder: may the source be with you!

The BigCode community, an open-scientific collaboration working on the responsible development of Large Language Models for Code (Code LLMs), introduces StarCoder and StarCoderBase: 15.5B parameter models with 8K context length, infilling capabilities and fast large-batch inference enabled by multi-query attention. StarCoderBase is trained on 1 trillion tokens sourced from The Stack, a large collection of permissively licensed GitHub repositories with inspection tools and an opt-out process. We fine-tuned StarCoderBase on 35B Python tokens, resulting in the creation of StarCoder. We perform the most comprehensive evaluation of Code LLMs to date and show that StarCoderBase outperforms every open Code LLM that supports multiple programming languages and matches or outperforms the OpenAI code-cushman-001 model. Furthermore, StarCoder outperforms every model that is fine-tuned on Python, can be prompted to achieve 40\% pass@1 on HumanEval, and still retains its performance on other programming languages. We take several important steps towards a safe open-access model release, including an improved PII redaction pipeline and a novel attribution tracing tool, and make the StarCoder models publicly available under a more commercially viable version of the Open Responsible AI Model license.

Implicit Regularization Towards Rank Minimization in ReLU Networks

We study the conjectured relationship between the implicit regularization in neural networks, trained with gradient-based methods, and rank minimization of their weight matrices. Previously, it was proved that for linear networks (of depth 2 and vector-valued outputs), gradient flow (GF) w.r.t. the square loss acts as a rank minimization heuristic. However, understanding to what extent this generalizes to nonlinear networks is an open problem. In this paper, we focus on nonlinear ReLU networks, providing several new positive and negative results. On the negative side, we prove (and demonstrate empirically) that, unlike the linear case, GF on ReLU networks may no longer tend to minimize ranks, in a rather strong sense (even approximately, for "most" datasets of size 2). On the positive side, we reveal that ReLU networks of sufficient depth are provably biased towards low-rank solutions in several reasonable settings.