Rethinking Link Prediction for Directed Graphs

Link prediction for directed graphs is a crucial task with diverse real-world applications. Recent advances in embedding methods and Graph Neural Networks (GNNs) have shown promising improvements. However, these methods often lack a thorough analysis of embedding expressiveness and suffer from ineffective benchmarks for a fair evaluation. In this paper, we propose a unified framework to assess the expressiveness of existing methods, highlighting the impact of dual embeddings and decoder design on performance. To address limitations in current experimental setups, we introduce DirLinkBench, a robust new benchmark with comprehensive coverage and standardized evaluation. The results show that current methods struggle to achieve strong performance on the new benchmark, while DiGAE outperforms others overall. We further revisit DiGAE theoretically, showing its graph convolution aligns with GCN on an undirected bipartite graph. Inspired by these insights, we propose a novel spectral directed graph auto-encoder SDGAE that achieves SOTA results on DirLinkBench. Finally, we analyze key factors influencing directed link prediction and highlight open challenges.

PolyFormer: Scalable Node-wise Filters via Polynomial Graph Transformer

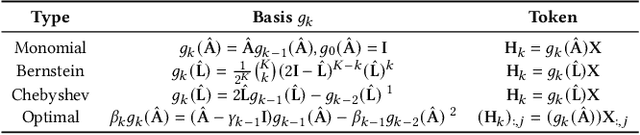
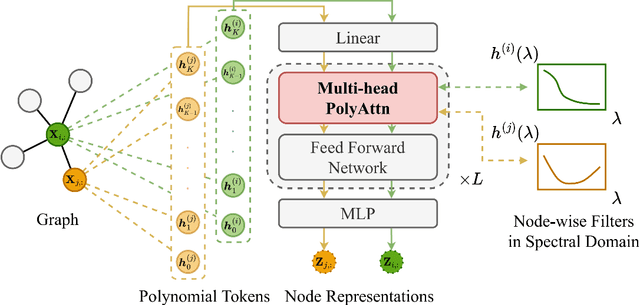
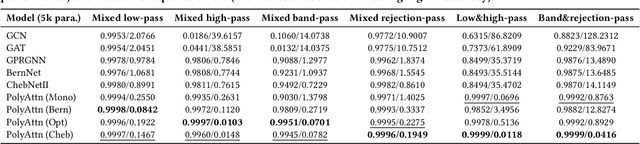
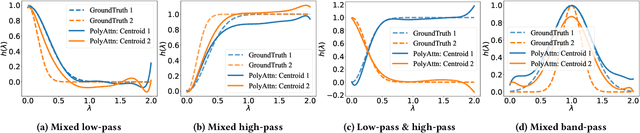
Spectral Graph Neural Networks have demonstrated superior performance in graph representation learning. However, many current methods focus on employing shared polynomial coefficients for all nodes, i.e., learning node-unified filters, which limits the filters' flexibility for node-level tasks. The recent DSF attempts to overcome this limitation by learning node-wise coefficients based on positional encoding. However, the initialization and updating process of the positional encoding are burdensome, hindering scalability on large-scale graphs. In this work, we propose a scalable node-wise filter, PolyAttn. Leveraging the attention mechanism, PolyAttn can directly learn node-wise filters in an efficient manner, offering powerful representation capabilities. Building on PolyAttn, we introduce the whole model, named PolyFormer. In the lens of Graph Transformer models, PolyFormer, which calculates attention scores within nodes, shows great scalability. Moreover, the model captures spectral information, enhancing expressiveness while maintaining efficiency. With these advantages, PolyFormer offers a desirable balance between scalability and expressiveness for node-level tasks. Extensive experiments demonstrate that our proposed methods excel at learning arbitrary node-wise filters, showing superior performance on both homophilic and heterophilic graphs, and handling graphs containing up to 100 million nodes. The code is available at https://github.com/air029/PolyFormer.

Spectral Heterogeneous Graph Convolutions via Positive Noncommutative Polynomials

Heterogeneous Graph Neural Networks (HGNNs) have gained significant popularity in various heterogeneous graph learning tasks. However, most HGNNs rely on spatial domain-based message passing and attention modules for information propagation and aggregation. These spatial-based HGNNs neglect the utilization of spectral graph convolutions, which are the foundation of Graph Convolutional Networks (GCN) on homogeneous graphs. Inspired by the effectiveness and scalability of spectral-based GNNs on homogeneous graphs, this paper explores the extension of spectral-based GNNs to heterogeneous graphs. We propose PSHGCN, a novel heterogeneous convolutional network based on positive noncommutative polynomials. PSHGCN provides a simple yet effective approach for learning spectral graph convolutions on heterogeneous graphs. Moreover, we demonstrate the rationale of PSHGCN in graph optimization. We conducted an extensive experimental study to show that PSHGCN can learn diverse spectral heterogeneous graph convolutions and achieve superior performance in node classification tasks. Our code is available at https://github.com/ivam-he/PSHGCN.

Convolutional Neural Networks on Graphs with Chebyshev Approximation, Revisited

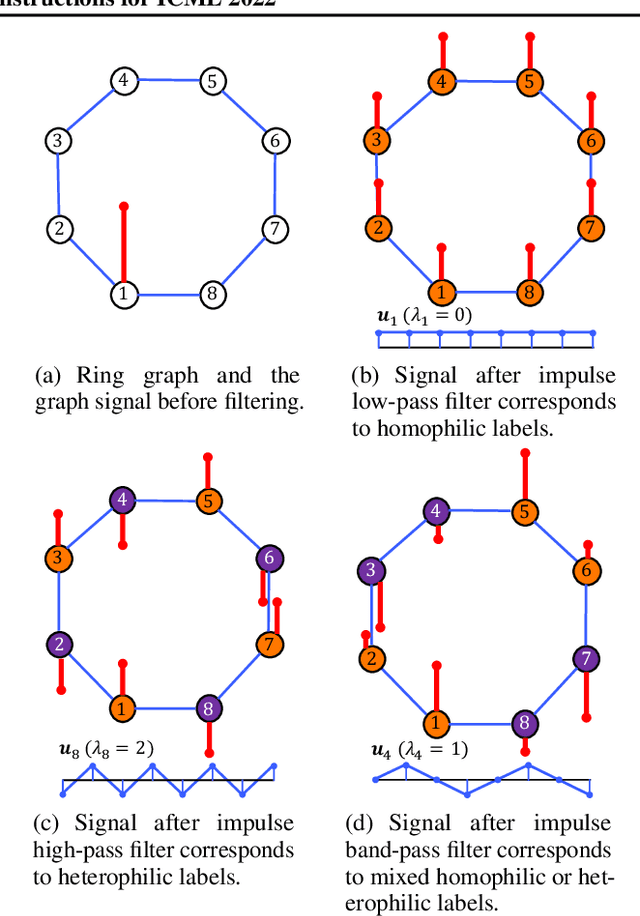
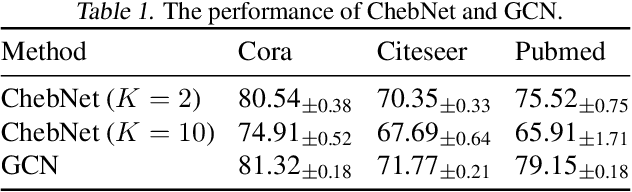
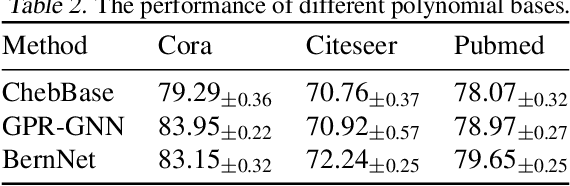
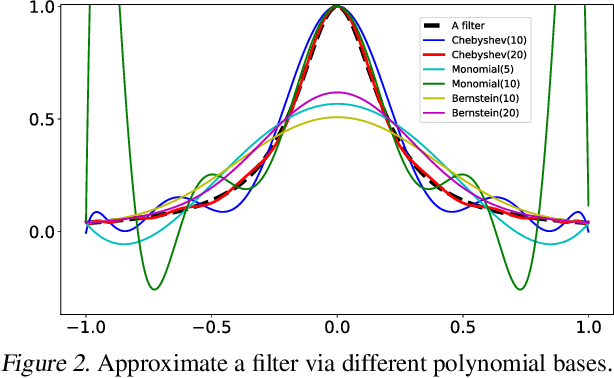
Designing spectral convolutional networks is a challenging problem in graph learning. ChebNet, one of the early attempts, approximates the spectral convolution using Chebyshev polynomials. GCN simplifies ChebNet by utilizing only the first two Chebyshev polynomials while still outperforming it on real-world datasets. GPR-GNN and BernNet demonstrate that the Monomial and Bernstein bases also outperform the Chebyshev basis in terms of learning the spectral convolution. Such conclusions are counter-intuitive in the field of approximation theory, where it is established that the Chebyshev polynomial achieves the optimum convergent rate for approximating a function. In this paper, we revisit the problem of approximating the spectral convolution with Chebyshev polynomials. We show that ChebNet's inferior performance is primarily due to illegal coefficients learnt by ChebNet approximating analytic filter functions, which leads to over-fitting. We then propose ChebNetII, a new GNN model based on Chebyshev interpolation, which enhances the original Chebyshev polynomial approximation while reducing the Runge phenomena. We conducted an extensive experimental study to demonstrate that ChebNetII can learn arbitrary graph spectrum filters and achieve superior performance in both full- and semi-supervised node classification tasks.

BernNet: Learning Arbitrary Graph Spectral Filters via Bernstein Approximation

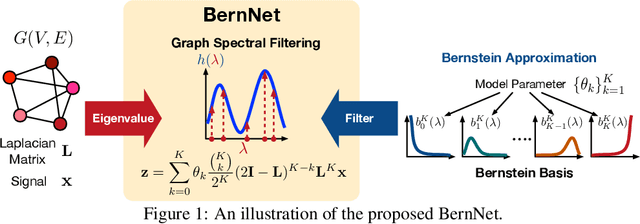
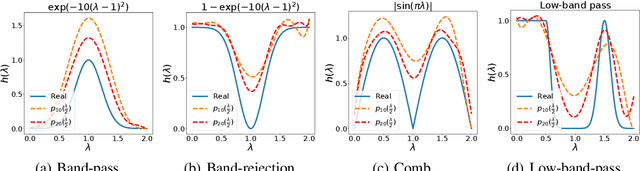
Many representative graph neural networks, $e.g.$, GPR-GNN and ChebyNet, approximate graph convolutions with graph spectral filters. However, existing work either applies predefined filter weights or learns them without necessary constraints, which may lead to oversimplified or ill-posed filters. To overcome these issues, we propose $\textit{BernNet}$, a novel graph neural network with theoretical support that provides a simple but effective scheme for designing and learning arbitrary graph spectral filters. In particular, for any filter over the normalized Laplacian spectrum of a graph, our BernNet estimates it by an order-$K$ Bernstein polynomial approximation and designs its spectral property by setting the coefficients of the Bernstein basis. Moreover, we can learn the coefficients (and the corresponding filter weights) based on observed graphs and their associated signals and thus achieve the BernNet specialized for the data. Our experiments demonstrate that BernNet can learn arbitrary spectral filters, including complicated band-rejection and comb filters, and it achieves superior performance in real-world graph modeling tasks.