Deep Symbolic Optimization: Reinforcement Learning for Symbolic Mathematics

Deep Symbolic Optimization (DSO) is a novel computational framework that enables symbolic optimization for scientific discovery, particularly in applications involving the search for intricate symbolic structures. One notable example is equation discovery, which aims to automatically derive mathematical models expressed in symbolic form. In DSO, the discovery process is formulated as a sequential decision-making task. A generative neural network learns a probabilistic model over a vast space of candidate symbolic expressions, while reinforcement learning strategies guide the search toward the most promising regions. This approach integrates gradient-based optimization with evolutionary and local search techniques, and it incorporates in-situ constraints, domain-specific priors, and advanced policy optimization methods. The result is a robust framework capable of efficiently exploring extensive search spaces to identify interpretable and physically meaningful models. Extensive evaluations on benchmark problems have demonstrated that DSO achieves state-of-the-art performance in both accuracy and interpretability. In this chapter, we provide a comprehensive overview of the DSO framework and illustrate its transformative potential for automating symbolic optimization in scientific discovery.

DisCo-DSO: Coupling Discrete and Continuous Optimization for Efficient Generative Design in Hybrid Spaces

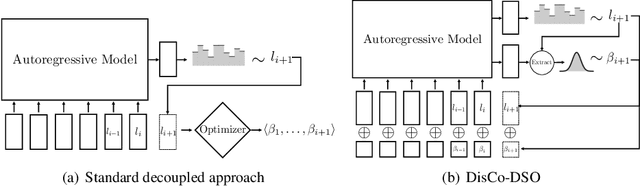
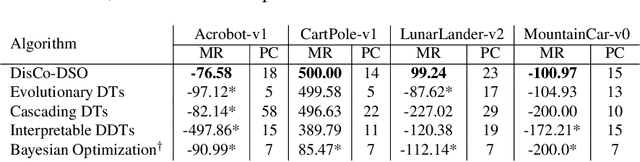
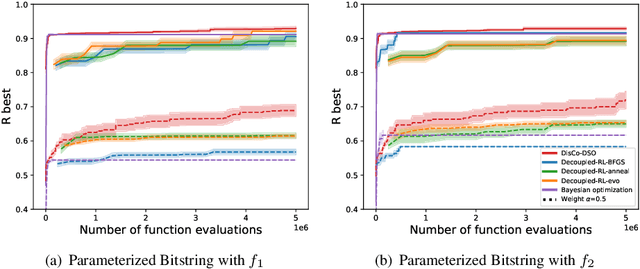
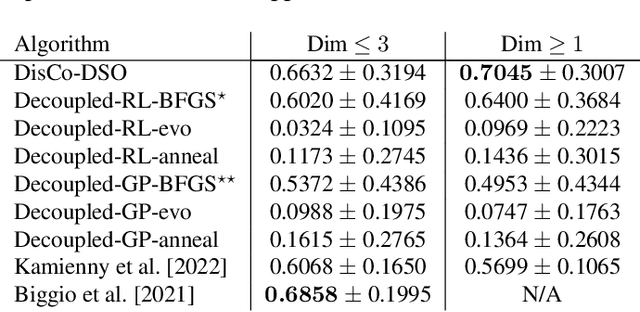
We consider the challenge of black-box optimization within hybrid discrete-continuous and variable-length spaces, a problem that arises in various applications, such as decision tree learning and symbolic regression. We propose DisCo-DSO (Discrete-Continuous Deep Symbolic Optimization), a novel approach that uses a generative model to learn a joint distribution over discrete and continuous design variables to sample new hybrid designs. In contrast to standard decoupled approaches, in which the discrete and continuous variables are optimized separately, our joint optimization approach uses fewer objective function evaluations, is robust against non-differentiable objectives, and learns from prior samples to guide the search, leading to significant improvement in performance and sample efficiency. Our experiments on a diverse set of optimization tasks demonstrate that the advantages of DisCo-DSO become increasingly evident as the complexity of the problem increases. In particular, we illustrate DisCo-DSO's superiority over the state-of-the-art methods for interpretable reinforcement learning with decision trees.

Symbolic Regression via Neural-Guided Genetic Programming Population Seeding

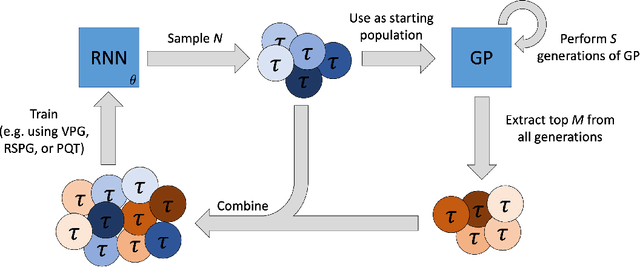
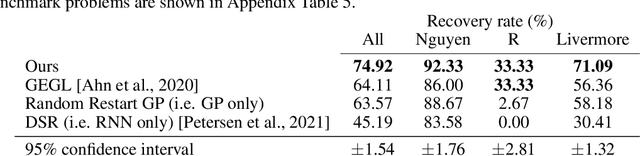
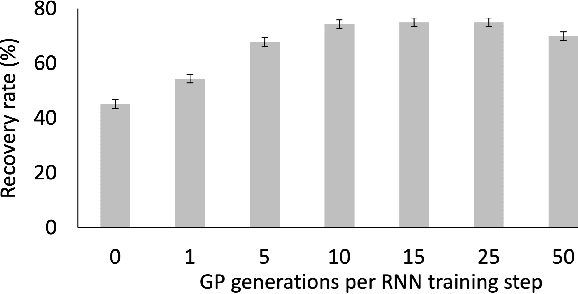
Symbolic regression is the process of identifying mathematical expressions that fit observed output from a black-box process. It is a discrete optimization problem generally believed to be NP-hard. Prior approaches to solving the problem include neural-guided search (e.g. using reinforcement learning) and genetic programming. In this work, we introduce a hybrid neural-guided/genetic programming approach to symbolic regression and other combinatorial optimization problems. We propose a neural-guided component used to seed the starting population of a random restart genetic programming component, gradually learning better starting populations. On a number of common benchmark tasks to recover underlying expressions from a dataset, our method recovers 65% more expressions than a recently published top-performing model using the same experimental setup. We demonstrate that running many genetic programming generations without interdependence on the neural-guided component performs better for symbolic regression than alternative formulations where the two are more strongly coupled. Finally, we introduce a new set of 22 symbolic regression benchmark problems with increased difficulty over existing benchmarks. Source code is provided at www.github.com/brendenpetersen/deep-symbolic-optimization.