DisCo-DSO: Coupling Discrete and Continuous Optimization for Efficient Generative Design in Hybrid Spaces

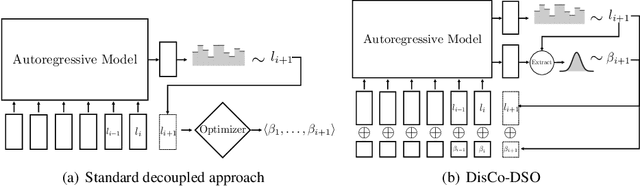
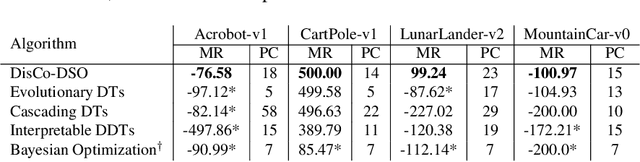
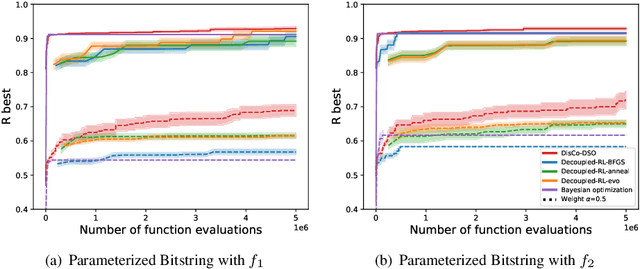
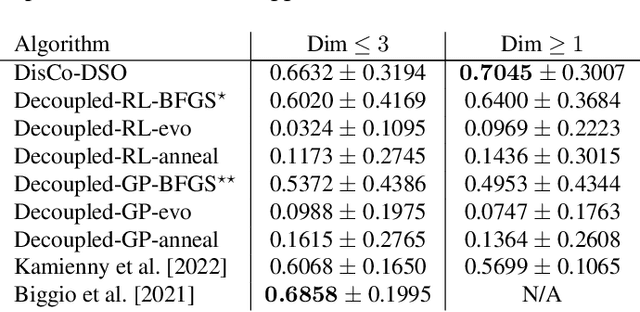
We consider the challenge of black-box optimization within hybrid discrete-continuous and variable-length spaces, a problem that arises in various applications, such as decision tree learning and symbolic regression. We propose DisCo-DSO (Discrete-Continuous Deep Symbolic Optimization), a novel approach that uses a generative model to learn a joint distribution over discrete and continuous design variables to sample new hybrid designs. In contrast to standard decoupled approaches, in which the discrete and continuous variables are optimized separately, our joint optimization approach uses fewer objective function evaluations, is robust against non-differentiable objectives, and learns from prior samples to guide the search, leading to significant improvement in performance and sample efficiency. Our experiments on a diverse set of optimization tasks demonstrate that the advantages of DisCo-DSO become increasingly evident as the complexity of the problem increases. In particular, we illustrate DisCo-DSO's superiority over the state-of-the-art methods for interpretable reinforcement learning with decision trees.

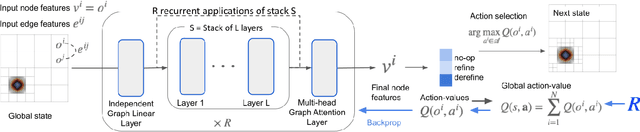
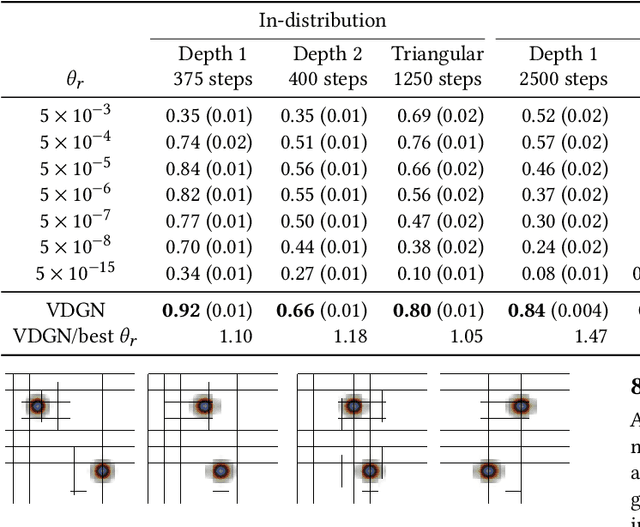
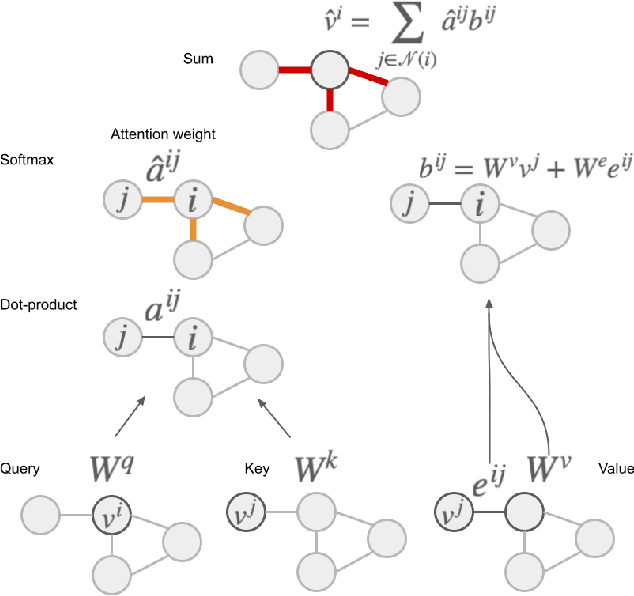
Multi-Agent Reinforcement Learning for Adaptive Mesh Refinement

Adaptive mesh refinement (AMR) is necessary for efficient finite element simulations of complex physical phenomenon, as it allocates limited computational budget based on the need for higher or lower resolution, which varies over space and time. We present a novel formulation of AMR as a fully-cooperative Markov game, in which each element is an independent agent who makes refinement and de-refinement choices based on local information. We design a novel deep multi-agent reinforcement learning (MARL) algorithm called Value Decomposition Graph Network (VDGN), which solves the two core challenges that AMR poses for MARL: posthumous credit assignment due to agent creation and deletion, and unstructured observations due to the diversity of mesh geometries. For the first time, we show that MARL enables anticipatory refinement of regions that will encounter complex features at future times, thereby unlocking entirely new regions of the error-cost objective landscape that are inaccessible by traditional methods based on local error estimators. Comprehensive experiments show that VDGN policies significantly outperform error threshold-based policies in global error and cost metrics. We show that learned policies generalize to test problems with physical features, mesh geometries, and longer simulation times that were not seen in training. We also extend VDGN with multi-objective optimization capabilities to find the Pareto front of the tradeoff between cost and error.

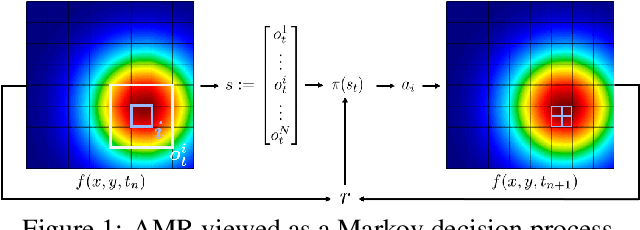
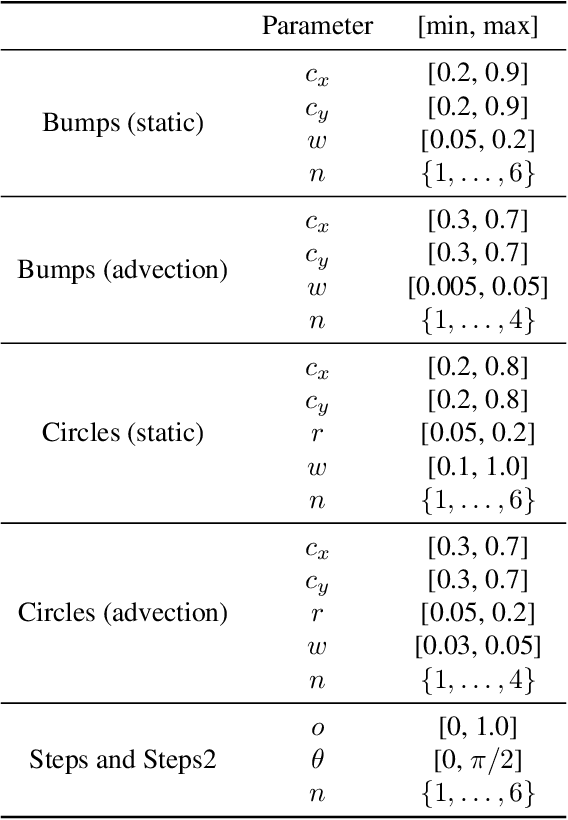
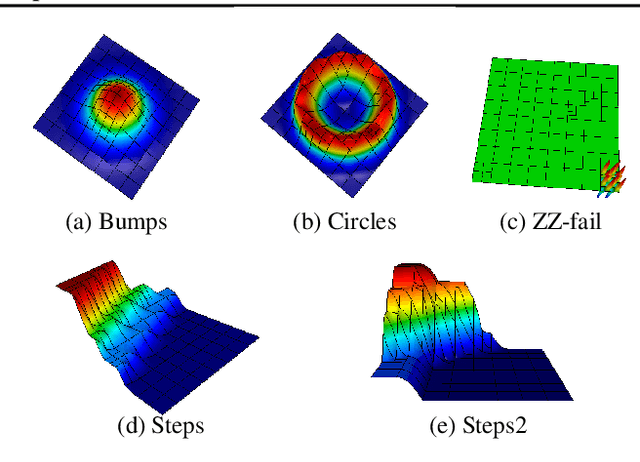
Reinforcement Learning for Adaptive Mesh Refinement

Large-scale finite element simulations of complex physical systems governed by partial differential equations crucially depend on adaptive mesh refinement (AMR) to allocate computational budget to regions where higher resolution is required. Existing scalable AMR methods make heuristic refinement decisions based on instantaneous error estimation and thus do not aim for long-term optimality over an entire simulation. We propose a novel formulation of AMR as a Markov decision process and apply deep reinforcement learning (RL) to train refinement policies directly from simulation. AMR poses a new problem for RL in that both the state dimension and available action set changes at every step, which we solve by proposing new policy architectures with differing generality and inductive bias. The model sizes of these policy architectures are independent of the mesh size and hence scale to arbitrarily large and complex simulations. We demonstrate in comprehensive experiments on static function estimation and the advection of different fields that RL policies can be competitive with a widely-used error estimator and generalize to larger, more complex, and unseen test problems.

Single Episode Policy Transfer in Reinforcement Learning

Transfer and adaptation to new unknown environmental dynamics is a key challenge for reinforcement learning (RL). An even greater challenge is performing near-optimally in a single attempt at test time, possibly without access to dense rewards, which is not addressed by current methods that require multiple experience rollouts for adaptation. To achieve single episode transfer in a family of environments with related dynamics, we propose a general algorithm that optimizes a probe and an inference model to rapidly estimate underlying latent variables of test dynamics, which are then immediately used as input to a universal control policy. This modular approach enables integration of state-of-the-art algorithms for variational inference or RL. Moreover, our approach does not require access to rewards at test time, allowing it to perform in settings where existing adaptive approaches cannot. In diverse experimental domains with a single episode test constraint, our method significantly outperforms existing adaptive approaches and shows favorable performance against baselines for robust transfer.