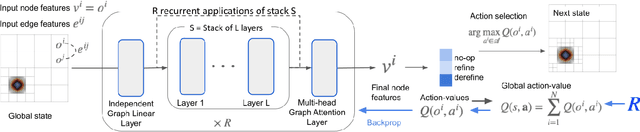
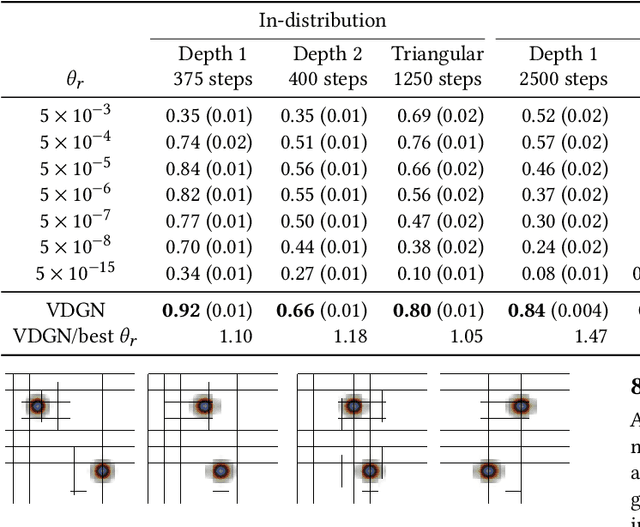
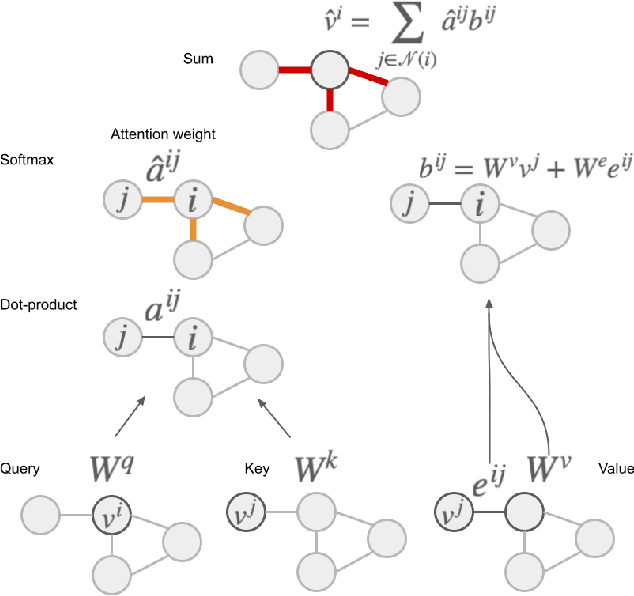
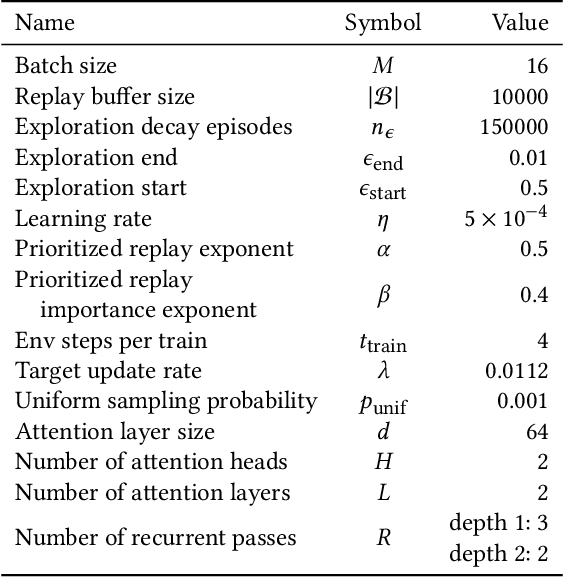
Multi-Agent Reinforcement Learning for Adaptive Mesh Refinement

Adaptive mesh refinement (AMR) is necessary for efficient finite element simulations of complex physical phenomenon, as it allocates limited computational budget based on the need for higher or lower resolution, which varies over space and time. We present a novel formulation of AMR as a fully-cooperative Markov game, in which each element is an independent agent who makes refinement and de-refinement choices based on local information. We design a novel deep multi-agent reinforcement learning (MARL) algorithm called Value Decomposition Graph Network (VDGN), which solves the two core challenges that AMR poses for MARL: posthumous credit assignment due to agent creation and deletion, and unstructured observations due to the diversity of mesh geometries. For the first time, we show that MARL enables anticipatory refinement of regions that will encounter complex features at future times, thereby unlocking entirely new regions of the error-cost objective landscape that are inaccessible by traditional methods based on local error estimators. Comprehensive experiments show that VDGN policies significantly outperform error threshold-based policies in global error and cost metrics. We show that learned policies generalize to test problems with physical features, mesh geometries, and longer simulation times that were not seen in training. We also extend VDGN with multi-objective optimization capabilities to find the Pareto front of the tradeoff between cost and error.

Learning robust marking policies for adaptive mesh refinement

In this work, we revisit the marking decisions made in the standard adaptive finite element method (AFEM). Experience shows that a na\"{i}ve marking policy leads to inefficient use of computational resources for adaptive mesh refinement (AMR). Consequently, using AFEM in practice often involves ad-hoc or time-consuming offline parameter tuning to set appropriate parameters for the marking subroutine. To address these practical concerns, we recast AMR as a Markov decision process in which refinement parameters can be selected on-the-fly at run time, without the need for pre-tuning by expert users. In this new paradigm, the refinement parameters are also chosen adaptively via a marking policy that can be optimized using methods from reinforcement learning. We use the Poisson equation to demonstrate our techniques on $h$- and $hp$-refinement benchmark problems, and our experiments suggest that superior marking policies remain undiscovered for many classical AFEM applications. Furthermore, an unexpected observation from this work is that marking policies trained on one family of PDEs are sometimes robust enough to perform well on problems far outside the training family. For illustration, we show that a simple $hp$-refinement policy trained on 2D domains with only a single re-entrant corner can be deployed on far more complicated 2D domains, and even 3D domains, without significant performance loss. For reproduction and broader adoption, we accompany this work with an open-source implementation of our methods.