Improving Explainability of Softmax Classifiers Using a Prototype-Based Joint Embedding Method

We propose a prototype-based approach for improving explainability of softmax classifiers that provides an understandable prediction confidence, generated through stochastic sampling of prototypes, and demonstrates potential for out of distribution detection (OOD). By modifying the model architecture and training to make predictions using similarities to any set of class examples from the training dataset, we acquire the ability to sample for prototypical examples that contributed to the prediction, which provide an instance-based explanation for the model's decision. Furthermore, by learning relationships between images from the training dataset through relative distances within the model's latent space, we obtain a metric for uncertainty that is better able to detect out of distribution data than softmax confidence.

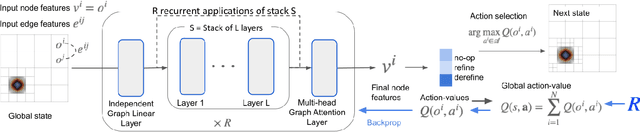
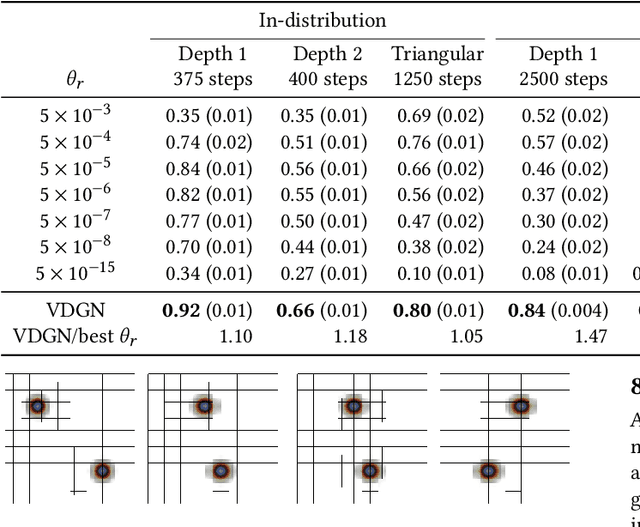
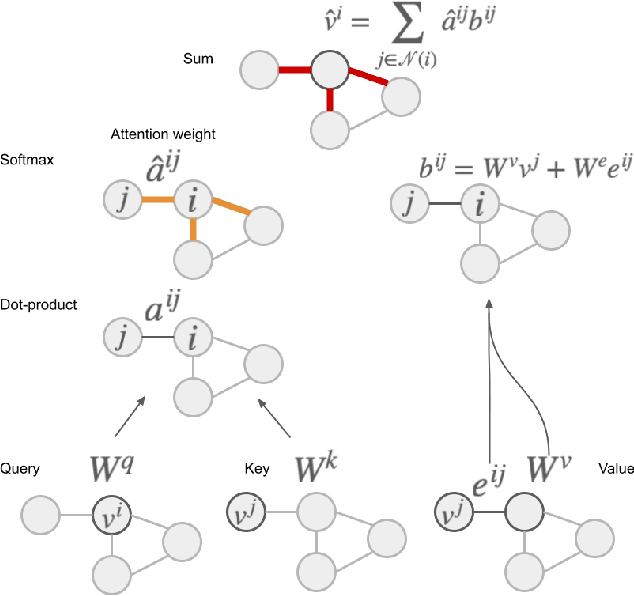
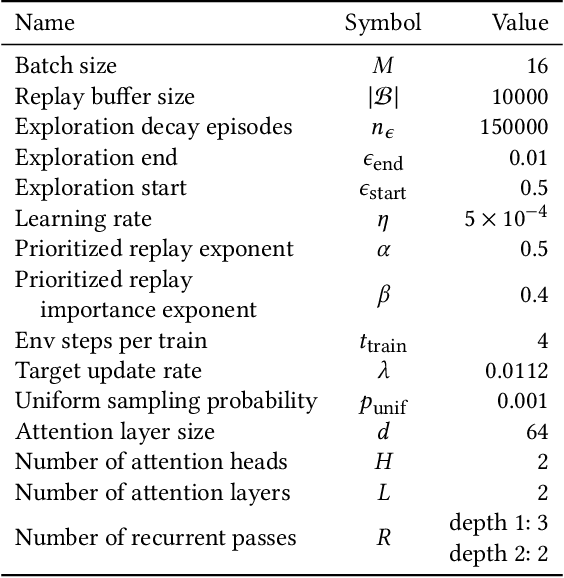
Multi-Agent Reinforcement Learning for Adaptive Mesh Refinement

Adaptive mesh refinement (AMR) is necessary for efficient finite element simulations of complex physical phenomenon, as it allocates limited computational budget based on the need for higher or lower resolution, which varies over space and time. We present a novel formulation of AMR as a fully-cooperative Markov game, in which each element is an independent agent who makes refinement and de-refinement choices based on local information. We design a novel deep multi-agent reinforcement learning (MARL) algorithm called Value Decomposition Graph Network (VDGN), which solves the two core challenges that AMR poses for MARL: posthumous credit assignment due to agent creation and deletion, and unstructured observations due to the diversity of mesh geometries. For the first time, we show that MARL enables anticipatory refinement of regions that will encounter complex features at future times, thereby unlocking entirely new regions of the error-cost objective landscape that are inaccessible by traditional methods based on local error estimators. Comprehensive experiments show that VDGN policies significantly outperform error threshold-based policies in global error and cost metrics. We show that learned policies generalize to test problems with physical features, mesh geometries, and longer simulation times that were not seen in training. We also extend VDGN with multi-objective optimization capabilities to find the Pareto front of the tradeoff between cost and error.

Learning robust marking policies for adaptive mesh refinement

In this work, we revisit the marking decisions made in the standard adaptive finite element method (AFEM). Experience shows that a na\"{i}ve marking policy leads to inefficient use of computational resources for adaptive mesh refinement (AMR). Consequently, using AFEM in practice often involves ad-hoc or time-consuming offline parameter tuning to set appropriate parameters for the marking subroutine. To address these practical concerns, we recast AMR as a Markov decision process in which refinement parameters can be selected on-the-fly at run time, without the need for pre-tuning by expert users. In this new paradigm, the refinement parameters are also chosen adaptively via a marking policy that can be optimized using methods from reinforcement learning. We use the Poisson equation to demonstrate our techniques on $h$- and $hp$-refinement benchmark problems, and our experiments suggest that superior marking policies remain undiscovered for many classical AFEM applications. Furthermore, an unexpected observation from this work is that marking policies trained on one family of PDEs are sometimes robust enough to perform well on problems far outside the training family. For illustration, we show that a simple $hp$-refinement policy trained on 2D domains with only a single re-entrant corner can be deployed on far more complicated 2D domains, and even 3D domains, without significant performance loss. For reproduction and broader adoption, we accompany this work with an open-source implementation of our methods.

Learning the structure of wind: A data-driven nonlocal turbulence model for the atmospheric boundary layer

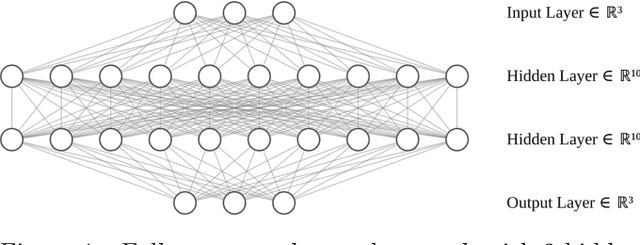
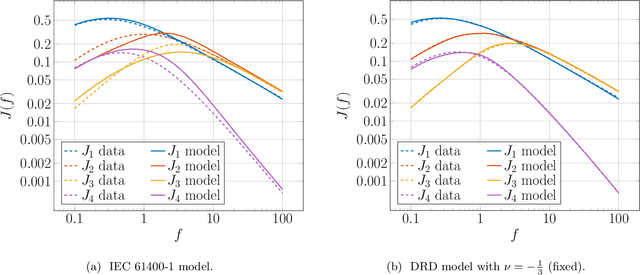
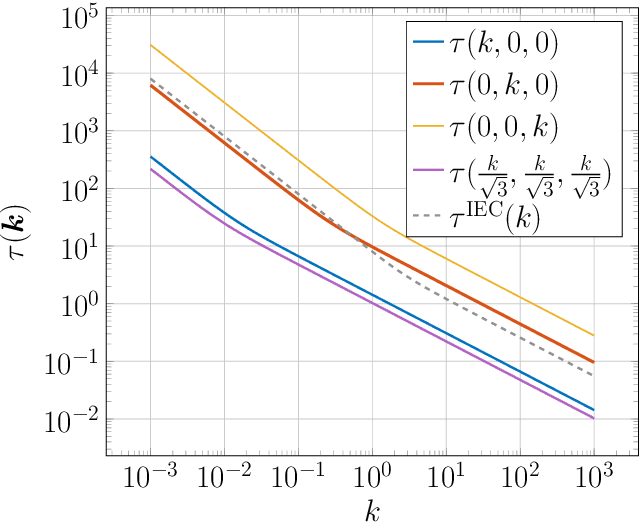
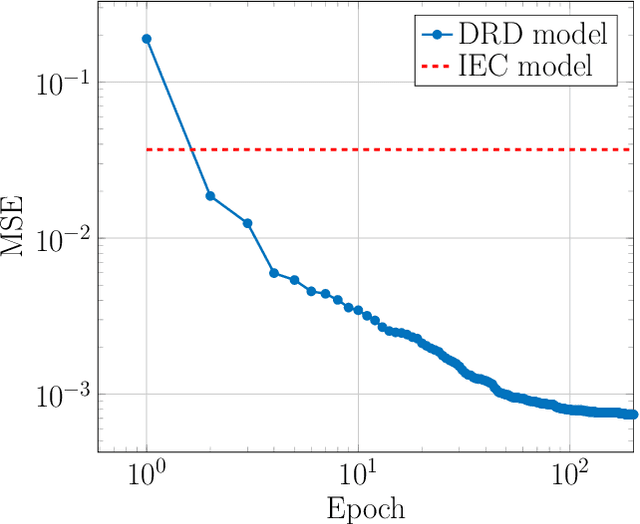
We develop a novel data-driven approach to modeling the atmospheric boundary layer. This approach leads to a nonlocal, anisotropic synthetic turbulence model which we refer to as the deep rapid distortion (DRD) model. Our approach relies on an operator regression problem which characterizes the best fitting candidate in a general family of nonlocal covariance kernels parameterized in part by a neural network. This family of covariance kernels is expressed in Fourier space and is obtained from approximate solutions to the Navier--Stokes equations at very high Reynolds numbers. Each member of the family incorporates important physical properties such as mass conservation and a realistic energy cascade. The DRD model can be calibrated with noisy data from field experiments. After calibration, the model can be used to generate synthetic turbulent velocity fields. To this end, we provide a new numerical method based on domain decomposition which delivers scalable, memory-efficient turbulence generation with the DRD model as well as others. We demonstrate the robustness of our approach with both filtered and noisy data coming from the 1968 Air Force Cambridge Research Laboratory Kansas experiments. Using this data, we witness exceptional accuracy with the DRD model, especially when compared to the International Electrotechnical Commission standard.

Orbital dynamics of binary black hole systems can be learned from gravitational wave measurements

We introduce a gravitational waveform inversion strategy that discovers mechanical models of binary black hole (BBH) systems. We show that only a single time series of (possibly noisy) waveform data is necessary to construct the equations of motion for a BBH system. Starting with a class of universal differential equations parameterized by feed-forward neural networks, our strategy involves the construction of a space of plausible mechanical models and a physics-informed constrained optimization within that space to minimize the waveform error. We apply our method to various BBH systems including extreme and comparable mass ratio systems in eccentric and non-eccentric orbits. We show the resulting differential equations apply to time durations longer than the training interval, and relativistic effects, such as perihelion precession, radiation reaction, and orbital plunge, are automatically accounted for. The methods outlined here provide a new, data-driven approach to studying the dynamics of binary black hole systems.