Leveraging Interpolation Models and Error Bounds for Verifiable Scientific Machine Learning

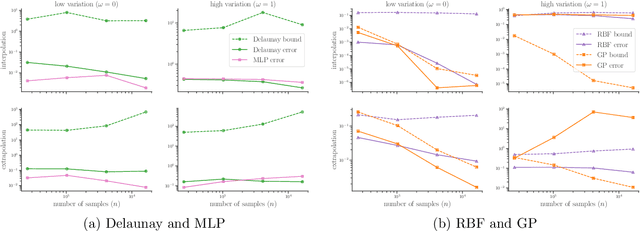
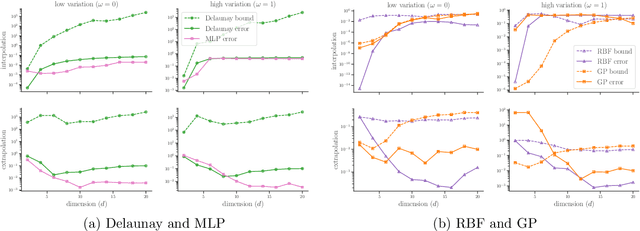
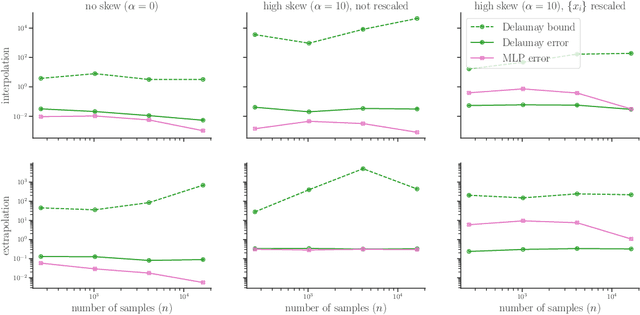
Effective verification and validation techniques for modern scientific machine learning workflows are challenging to devise. Statistical methods are abundant and easily deployed, but often rely on speculative assumptions about the data and methods involved. Error bounds for classical interpolation techniques can provide mathematically rigorous estimates of accuracy, but often are difficult or impractical to determine computationally. In this work, we present a best-of-both-worlds approach to verifiable scientific machine learning by demonstrating that (1) multiple standard interpolation techniques have informative error bounds that can be computed or estimated efficiently; (2) comparative performance among distinct interpolants can aid in validation goals; (3) deploying interpolation methods on latent spaces generated by deep learning techniques enables some interpretability for black-box models. We present a detailed case study of our approach for predicting lift-drag ratios from airfoil images. Code developed for this work is available in a public Github repository.

Learning robust marking policies for adaptive mesh refinement

In this work, we revisit the marking decisions made in the standard adaptive finite element method (AFEM). Experience shows that a na\"{i}ve marking policy leads to inefficient use of computational resources for adaptive mesh refinement (AMR). Consequently, using AFEM in practice often involves ad-hoc or time-consuming offline parameter tuning to set appropriate parameters for the marking subroutine. To address these practical concerns, we recast AMR as a Markov decision process in which refinement parameters can be selected on-the-fly at run time, without the need for pre-tuning by expert users. In this new paradigm, the refinement parameters are also chosen adaptively via a marking policy that can be optimized using methods from reinforcement learning. We use the Poisson equation to demonstrate our techniques on $h$- and $hp$-refinement benchmark problems, and our experiments suggest that superior marking policies remain undiscovered for many classical AFEM applications. Furthermore, an unexpected observation from this work is that marking policies trained on one family of PDEs are sometimes robust enough to perform well on problems far outside the training family. For illustration, we show that a simple $hp$-refinement policy trained on 2D domains with only a single re-entrant corner can be deployed on far more complicated 2D domains, and even 3D domains, without significant performance loss. For reproduction and broader adoption, we accompany this work with an open-source implementation of our methods.