Symbolic Regression via Neural-Guided Genetic Programming Population Seeding

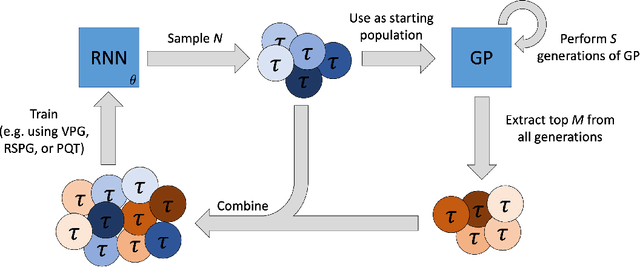
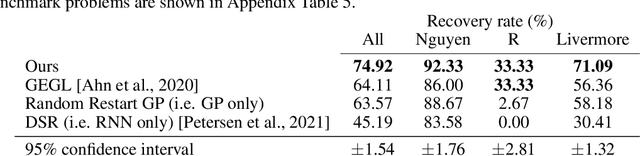
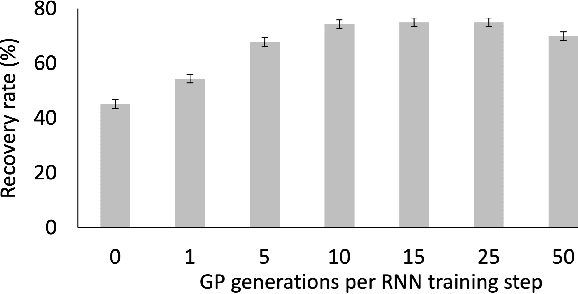
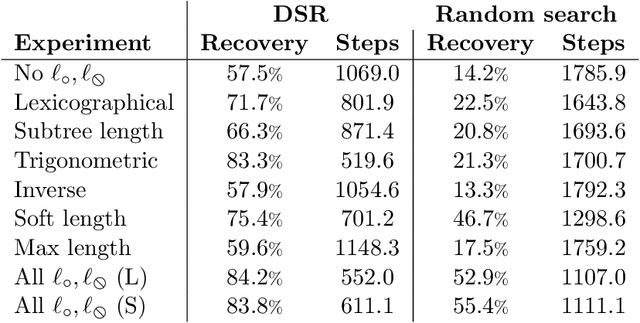
Symbolic regression is the process of identifying mathematical expressions that fit observed output from a black-box process. It is a discrete optimization problem generally believed to be NP-hard. Prior approaches to solving the problem include neural-guided search (e.g. using reinforcement learning) and genetic programming. In this work, we introduce a hybrid neural-guided/genetic programming approach to symbolic regression and other combinatorial optimization problems. We propose a neural-guided component used to seed the starting population of a random restart genetic programming component, gradually learning better starting populations. On a number of common benchmark tasks to recover underlying expressions from a dataset, our method recovers 65% more expressions than a recently published top-performing model using the same experimental setup. We demonstrate that running many genetic programming generations without interdependence on the neural-guided component performs better for symbolic regression than alternative formulations where the two are more strongly coupled. Finally, we introduce a new set of 22 symbolic regression benchmark problems with increased difficulty over existing benchmarks. Source code is provided at www.github.com/brendenpetersen/deep-symbolic-optimization.

Incorporating domain knowledge into neural-guided search

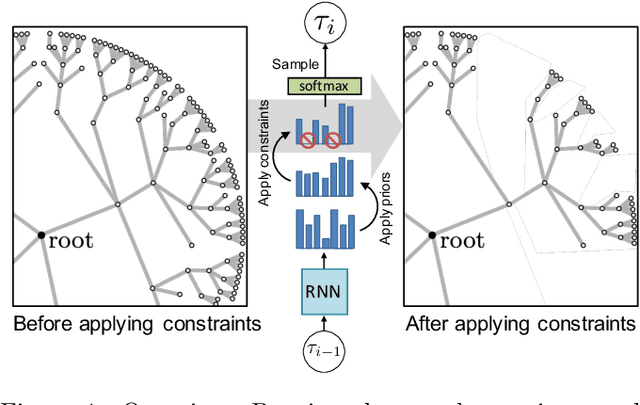
Many AutoML problems involve optimizing discrete objects under a black-box reward. Neural-guided search provides a flexible means of searching these combinatorial spaces using an autoregressive recurrent neural network. A major benefit of this approach is that builds up objects sequentially--this provides an opportunity to incorporate domain knowledge into the search by directly modifying the logits emitted during sampling. In this work, we formalize a framework for incorporating such in situ priors and constraints into neural-guided search, and provide sufficient conditions for enforcing constraints. We integrate several priors and constraints from existing works into this framework, propose several new ones, and demonstrate their efficacy in informing the task of symbolic regression.

Improving exploration in policy gradient search: Application to symbolic optimization

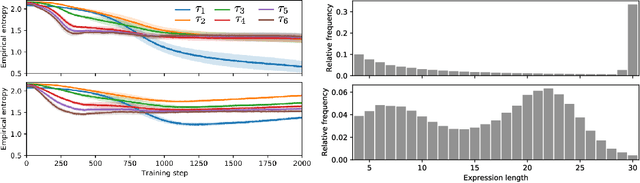
Many machine learning strategies designed to automate mathematical tasks leverage neural networks to search large combinatorial spaces of mathematical symbols. In contrast to traditional evolutionary approaches, using a neural network at the core of the search allows learning higher-level symbolic patterns, providing an informed direction to guide the search. When no labeled data is available, such networks can still be trained using reinforcement learning. However, we demonstrate that this approach can suffer from an early commitment phenomenon and from initialization bias, both of which limit exploration. We present two exploration methods to tackle these issues, building upon ideas of entropy regularization and distribution initialization. We show that these techniques can improve the performance, increase sample efficiency, and lower the complexity of solutions for the task of symbolic regression.