Mathias Berglund
Regularizing Trajectory Optimization with Denoising Autoencoders
Mar 28, 2019

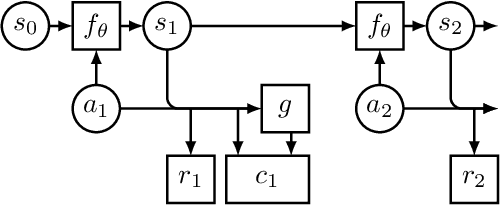

Abstract:Trajectory optimization with learned dynamics models can often suffer from erroneous predictions of out-of-distribution trajectories. We propose to regularize trajectory optimization by means of a denoising autoencoder that is trained on the same trajectories as the dynamics model. We visually demonstrate the effectiveness of the regularization in gradient-based trajectory optimization for open-loop control of an industrial process. We compare with recent model-based reinforcement learning algorithms on a set of popular motor control tasks to demonstrate that the denoising regularization enables state-of-the-art sample-efficiency. We demonstrate the efficacy of the proposed method in regularizing both gradient-based and gradient-free trajectory optimization.
Tagger: Deep Unsupervised Perceptual Grouping
Nov 28, 2016

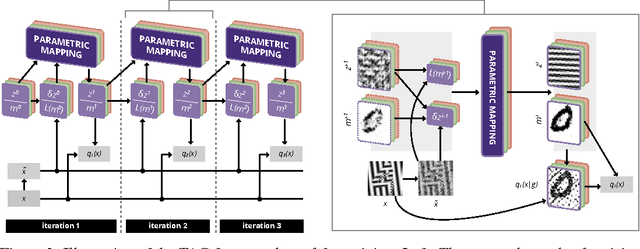
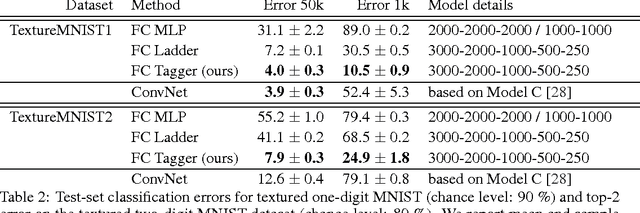
Abstract:We present a framework for efficient perceptual inference that explicitly reasons about the segmentation of its inputs and features. Rather than being trained for any specific segmentation, our framework learns the grouping process in an unsupervised manner or alongside any supervised task. By enriching the representations of a neural network, we enable it to group the representations of different objects in an iterative manner. By allowing the system to amortize the iterative inference of the groupings, we achieve very fast convergence. In contrast to many other recently proposed methods for addressing multi-object scenes, our system does not assume the inputs to be images and can therefore directly handle other modalities. For multi-digit classification of very cluttered images that require texture segmentation, our method offers improved classification performance over convolutional networks despite being fully connected. Furthermore, we observe that our system greatly improves on the semi-supervised result of a baseline Ladder network on our dataset, indicating that segmentation can also improve sample efficiency.
Scalable Gradient-Based Tuning of Continuous Regularization Hyperparameters
Jun 17, 2016



Abstract:Hyperparameter selection generally relies on running multiple full training trials, with selection based on validation set performance. We propose a gradient-based approach for locally adjusting hyperparameters during training of the model. Hyperparameters are adjusted so as to make the model parameter gradients, and hence updates, more advantageous for the validation cost. We explore the approach for tuning regularization hyperparameters and find that in experiments on MNIST, SVHN and CIFAR-10, the resulting regularization levels are within the optimal regions. The additional computational cost depends on how frequently the hyperparameters are trained, but the tested scheme adds only 30% computational overhead regardless of the model size. Since the method is significantly less computationally demanding compared to similar gradient-based approaches to hyperparameter optimization, and consistently finds good hyperparameter values, it can be a useful tool for training neural network models.
Semi-Supervised Learning with Ladder Networks
Nov 24, 2015
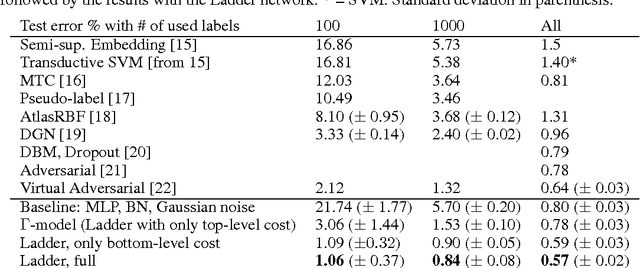


Abstract:We combine supervised learning with unsupervised learning in deep neural networks. The proposed model is trained to simultaneously minimize the sum of supervised and unsupervised cost functions by backpropagation, avoiding the need for layer-wise pre-training. Our work builds on the Ladder network proposed by Valpola (2015), which we extend by combining the model with supervision. We show that the resulting model reaches state-of-the-art performance in semi-supervised MNIST and CIFAR-10 classification, in addition to permutation-invariant MNIST classification with all labels.
Bidirectional Recurrent Neural Networks as Generative Models - Reconstructing Gaps in Time Series
Nov 02, 2015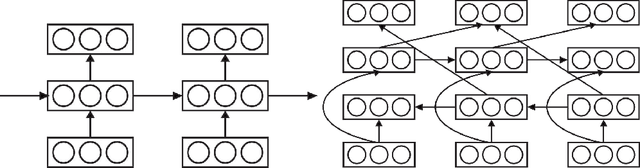

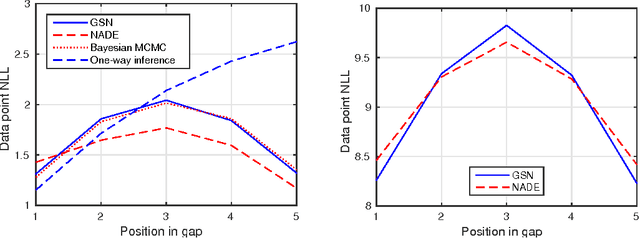
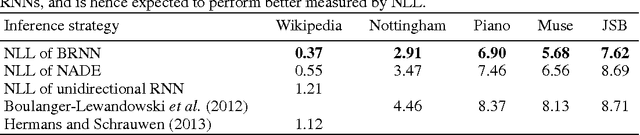
Abstract:Bidirectional recurrent neural networks (RNN) are trained to predict both in the positive and negative time directions simultaneously. They have not been used commonly in unsupervised tasks, because a probabilistic interpretation of the model has been difficult. Recently, two different frameworks, GSN and NADE, provide a connection between reconstruction and probabilistic modeling, which makes the interpretation possible. As far as we know, neither GSN or NADE have been studied in the context of time series before. As an example of an unsupervised task, we study the problem of filling in gaps in high-dimensional time series with complex dynamics. Although unidirectional RNNs have recently been trained successfully to model such time series, inference in the negative time direction is non-trivial. We propose two probabilistic interpretations of bidirectional RNNs that can be used to reconstruct missing gaps efficiently. Our experiments on text data show that both proposed methods are much more accurate than unidirectional reconstructions, although a bit less accurate than a computationally complex bidirectional Bayesian inference on the unidirectional RNN. We also provide results on music data for which the Bayesian inference is computationally infeasible, demonstrating the scalability of the proposed methods.
Techniques for Learning Binary Stochastic Feedforward Neural Networks
Apr 09, 2015



Abstract:Stochastic binary hidden units in a multi-layer perceptron (MLP) network give at least three potential benefits when compared to deterministic MLP networks. (1) They allow to learn one-to-many type of mappings. (2) They can be used in structured prediction problems, where modeling the internal structure of the output is important. (3) Stochasticity has been shown to be an excellent regularizer, which makes generalization performance potentially better in general. However, training stochastic networks is considerably more difficult. We study training using M samples of hidden activations per input. We show that the case M=1 leads to a fundamentally different behavior where the network tries to avoid stochasticity. We propose two new estimators for the training gradient and propose benchmark tests for comparing training algorithms. Our experiments confirm that training stochastic networks is difficult and show that the proposed two estimators perform favorably among all the five known estimators.
Stochastic Gradient Estimate Variance in Contrastive Divergence and Persistent Contrastive Divergence
Feb 14, 2014


Abstract:Contrastive Divergence (CD) and Persistent Contrastive Divergence (PCD) are popular methods for training the weights of Restricted Boltzmann Machines. However, both methods use an approximate method for sampling from the model distribution. As a side effect, these approximations yield significantly different biases and variances for stochastic gradient estimates of individual data points. It is well known that CD yields a biased gradient estimate. In this paper we however show empirically that CD has a lower stochastic gradient estimate variance than exact sampling, while the mean of subsequent PCD estimates has a higher variance than exact sampling. The results give one explanation to the finding that CD can be used with smaller minibatches or higher learning rates than PCD.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge