Adaptive Anomaly Detection in Network Flows with Low-Rank Tensor Decompositions and Deep Unrolling

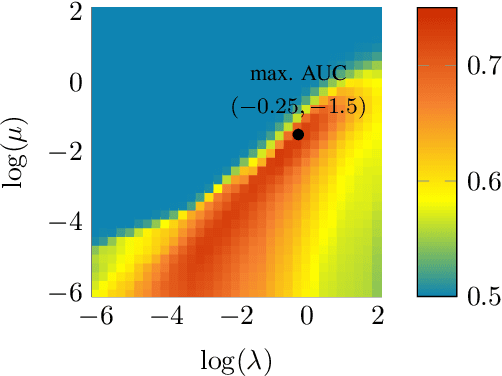
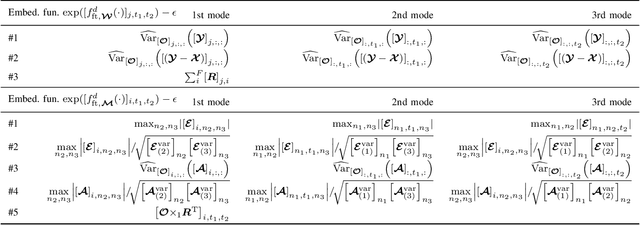
Anomaly detection (AD) is increasingly recognized as a key component for ensuring the resilience of future communication systems. While deep learning has shown state-of-the-art AD performance, its application in critical systems is hindered by concerns regarding training data efficiency, domain adaptation and interpretability. This work considers AD in network flows using incomplete measurements, leveraging a robust tensor decomposition approach and deep unrolling techniques to address these challenges. We first propose a novel block-successive convex approximation algorithm based on a regularized model-fitting objective where the normal flows are modeled as low-rank tensors and anomalies as sparse. An augmentation of the objective is introduced to decrease the computational cost. We apply deep unrolling to derive a novel deep network architecture based on our proposed algorithm, treating the regularization parameters as learnable weights. Inspired by Bayesian approaches, we extend the model architecture to perform online adaptation to per-flow and per-time-step statistics, improving AD performance while maintaining a low parameter count and preserving the problem's permutation equivariances. To optimize the deep network weights for detection performance, we employ a homotopy optimization approach based on an efficient approximation of the area under the receiver operating characteristic curve. Extensive experiments on synthetic and real-world data demonstrate that our proposed deep network architecture exhibits a high training data efficiency, outperforms reference methods, and adapts seamlessly to varying network topologies.

Decentralized Singular Value Decomposition for Extremely Large-scale Antenna Array Systems

In this article, the problems of decentralized Singular Value Decomposition (d-SVD) and decentralized Principal Component Analysis (d-PCA) are studied, which are fundamental in various signal processing applications. Two scenarios of d-SVD are considered depending on the availability of the data matrix under consideration. In the first scenario, the matrix of interest is row-wisely available in each local node in the network. In the second scenario, the matrix of interest implicitly forms an outer product generated from two different series of measurements. Combining the lightweight local rational function approximation approach and parallel averaging consensus algorithms, two d-SVD algorithms are proposed to cope with the two aforementioned scenarios. We demonstrate the proposed algorithms with two respective application examples for Extremely Large-scale Antenna Array (ELAA) systems: decentralized sensor localization via low-rank matrix completion and decentralized passive radar detection. Moreover, a non-trivial truncation technique, which employs a representative vector that is orthonormal to the principal signal subspace, is proposed to further reduce the associated communication cost with the d-SVD algorithms. Simulation results show that the proposed d-SVD algorithms converge to the centralized solution with reduced communication cost compared to those facilitated with the state-of-the-art decentralized power method.

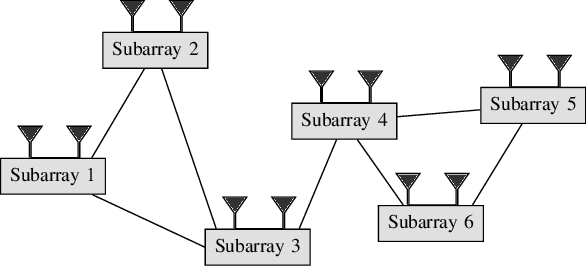
Gridless Parameter Estimation in Partly Calibrated Rectangular Arrays

Spatial frequency estimation from a mixture of noisy sinusoids finds applications in various fields. While subspace-based methods offer cost-effective super-resolution parameter estimation, they demand precise array calibration, posing challenges for large antennas. In contrast, sparsity-based approaches outperform subspace methods, especially in scenarios with limited snapshots or correlated sources. This study focuses on direction-of-arrival (DOA) estimation using a partly calibrated rectangular array with fully calibrated subarrays. A gridless sparse formulation leveraging shift invariances in the array is developed, yielding two competitive algorithms under the alternating direction method of multipliers (ADMM) and successive convex approximation frameworks, respectively. Numerical simulations show the superior error performance of our proposed method, particularly in highly correlated scenarios, compared to the conventional subspace-based methods. It is demonstrated that the proposed formulation can also be adopted in the fully calibrated case to improve the robustness of the subspace-based methods to the source correlation. Furthermore, we provide a generalization of the proposed method to a more challenging case where a part of the sensors is unobservable due to failures.

A tensor model for calibration and imaging with air-coupled ultrasonic sensor arrays

Arrays of ultrasonic sensors are capable of 3D imaging in air and an affordable supplement to other sensing modalities, such as radar, lidar, and camera, i.e. in heterogeneous sensing systems. However, manufacturing tolerances of air-coupled ultrasonic sensors may lead to amplitude and phase deviations. Together with artifacts from imperfect knowledge of the array geometry, there are numerous factors that can impair the imaging performance of an array. We propose a reference-based calibration method to overcome possible limitations. First, we introduce a novel tensor signal model to capture the characteristics of piezoelectric ultrasonic transducers (PUTs) and the underlying multidimensional nature of a multiple-input multiple-output (MIMO) sensor array. Second, we formulate an optimization problem based on the proposed tensor model to obtain the calibrated parameters of the array and solve the problem using a modified block coordinate descent (BCD) method. Third, we assess both our model and the commonly used analytical model using real data from a 3D imaging experiment. The experiment reveals that our array response model we learned with calibration data yields an imaging performance similar to that of the analytical array model, which requires perfect array geometry information.

Joint Sparse Estimation with Cardinality Constraint via Mixed-Integer Semidefinite Programming

The multiple measurement vectors (MMV) problem refers to the joint estimation of a row-sparse signal matrix from multiple realizations of mixtures with a known dictionary. As a generalization of the standard sparse representation problem for a single measurement, this problem is fundamental in various applications in signal processing, e.g., spectral analysis and direction-of-arrival (DOA) estimation. In this paper, we consider the maximum a posteriori (MAP) estimation for the MMV problem, which is classically formulated as a regularized least-squares (LS) problem with an $\ell_{2,0}$-norm constraint, and derive an equivalent mixed-integer semidefinite program (MISDP) reformulation. The proposed MISDP reformulation can be exactly solved by a generic MISDP solver, which, however, becomes computationally demanding for problems of extremely large dimensions. To further reduce the computation time in such scenarios, a relaxation-based approach can be employed to obtain an approximate solution of the MISDP reformulation, at the expense of a reduced estimation performance. Numerical simulations in the context of DOA estimation demonstrate the improved error performance of our proposed method in comparison to several popular DOA estimation methods. In particular, compared to the deterministic maximum likelihood (DML) estimator, which is often used as a benchmark, the proposed method applied with a state-of-the-art MISDP solver exhibits a superior estimation performance at a significantly reduced running time. Moreover, unlike other nonconvex approaches for the MMV problem, including the greedy methods and the sparse Bayesian learning, the proposed MISDP-based method offers a guarantee of finding a global optimum.

Three more Decades in Array Signal Processing Research: An Optimization and Structure Exploitation Perspective

The signal processing community currently witnesses the emergence of sensor array processing and Direction-of-Arrival (DoA) estimation in various modern applications, such as automotive radar, mobile user and millimeter wave indoor localization, drone surveillance, as well as in new paradigms, such as joint sensing and communication in future wireless systems. This trend is further enhanced by technology leaps and availability of powerful and affordable multi-antenna hardware platforms. The history of advances in super resolution DoA estimation techniques is long, starting from the early parametric multi-source methods such as the computationally expensive maximum likelihood (ML) techniques to the early subspace-based techniques such as Pisarenko and MUSIC. Inspired by the seminal review paper Two Decades of Array Signal Processing Research: The Parametric Approach by Krim and Viberg published in the IEEE Signal Processing Magazine, we are looking back at another three decades in Array Signal Processing Research under the classical narrowband array processing model based on second order statistics. We revisit major trends in the field and retell the story of array signal processing from a modern optimization and structure exploitation perspective. In our overview, through prominent examples, we illustrate how different DoA estimation methods can be cast as optimization problems with side constraints originating from prior knowledge regarding the structure of the measurement system. Due to space limitations, our review of the DoA estimation research in the past three decades is by no means complete. For didactic reasons, we mainly focus on developments in the field that easily relate the traditional multi-source estimation criteria and choose simple illustrative examples.

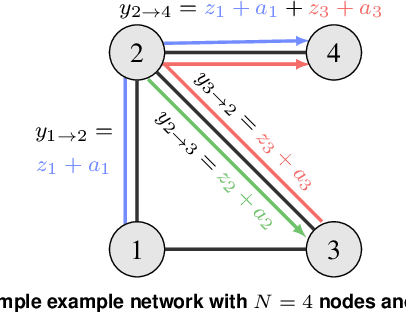
Decentralized Eigendecomposition for Online Learning over Graphs with Applications

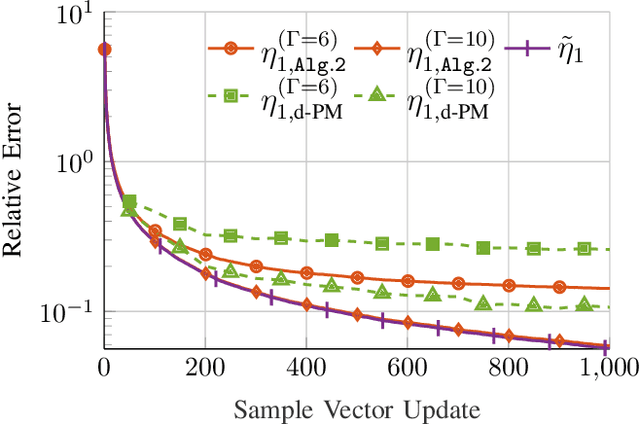
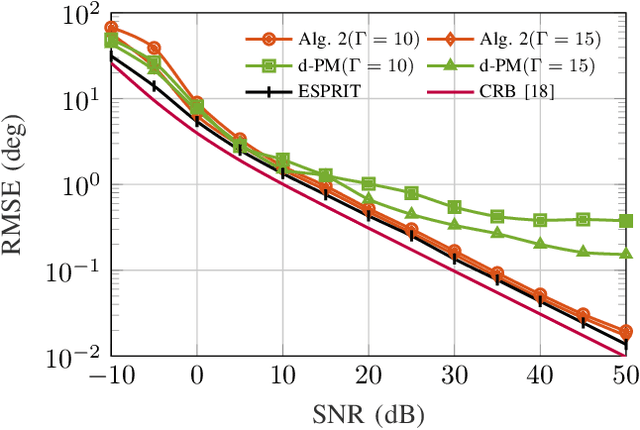
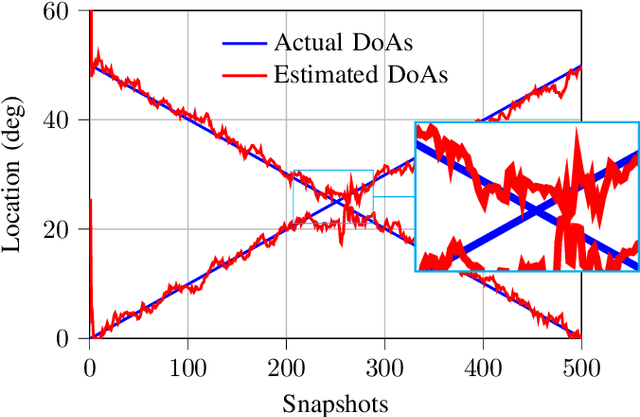
In this paper, the problem of decentralized eigenvalue decomposition of a general symmetric matrix that is important, e.g., in Principal Component Analysis, is studied, and a decentralized online learning algorithm is proposed. Instead of collecting all information in a fusion center, the proposed algorithm involves only local interactions among adjacent agents. It benefits from the representation of the matrix as a sum of rank-one components which makes the algorithm attractive for online eigenvalue and eigenvector tracking applications. We examine the performance of the proposed algorithm in two types of important application examples: First, we consider the online eigendecomposition of a sample covariance matrix over the network, with application in decentralized Direction-of-Arrival (DoA) estimation and DoA tracking applications. Then, we investigate the online computation of the spectra of the graph Laplacian that is important in, e.g., Graph Fourier Analysis and graph dependent filter design. We apply our proposed algorithm to track the spectra of the graph Laplacian in static and dynamic networks. Simulation results reveal that the proposed algorithm outperforms existing decentralized algorithms both in terms of estimation accuracy as well as communication cost.

Coordinated Sum-Rate Maximization in Multicell MU-MIMO with Deep Unrolling

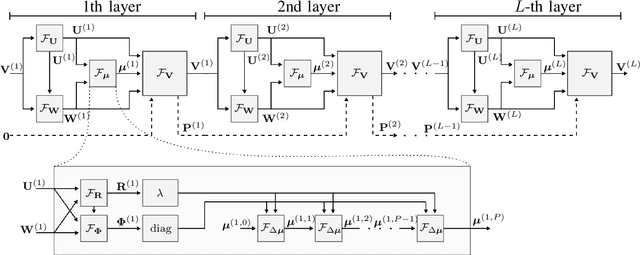
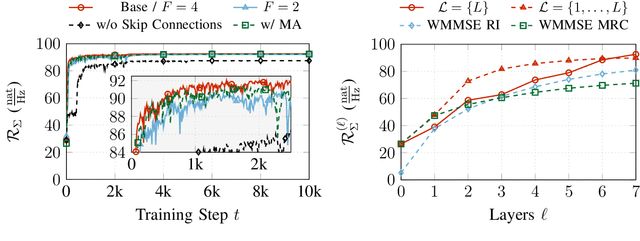
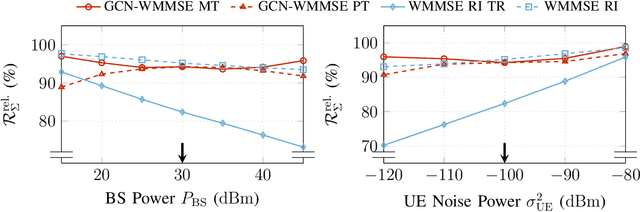
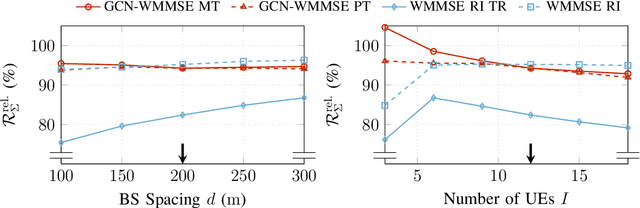
Coordinated weighted sum-rate maximization in multicell MIMO networks with intra- and intercell interference and local channel state at the base stations is recognized as an important yet difficult problem. A classical, locally optimal solution is obtained by the weighted minimum mean squared error (WMMSE) algorithm which facilitates a distributed implementation in multicell networks. However, it often suffers from slow convergence and therefore large communication overhead. To obtain more practical solutions, the unrolling/unfolding of traditional iterative algorithms gained significant attention. In this work, we demonstrate a complete unfolding of the WMMSE algorithm for transceiver design in multicell MU-MIMO interference channels with local channel state information. The resulting architecture termed GCN-WMMSE applies ideas from graph signal processing and is agnostic to different wireless network topologies, while exhibiting a low number of trainable parameters and high efficiency w.r.t. training data. It significantly reduces the number of required iterations while achieving performance similar to the WMMSE algorithm, alleviating the overhead in a distributed deployment. Additionally, we review previous architectures based on unrolling the WMMSE algorithm and compare them to GCN-WMMSE in their specific applicable domains.

Ambiguities in Direction-of-Arrival Estimation with Linear Arrays

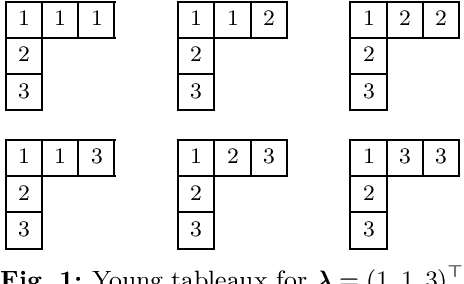
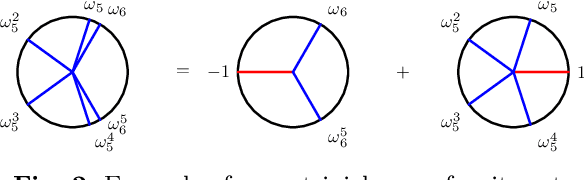
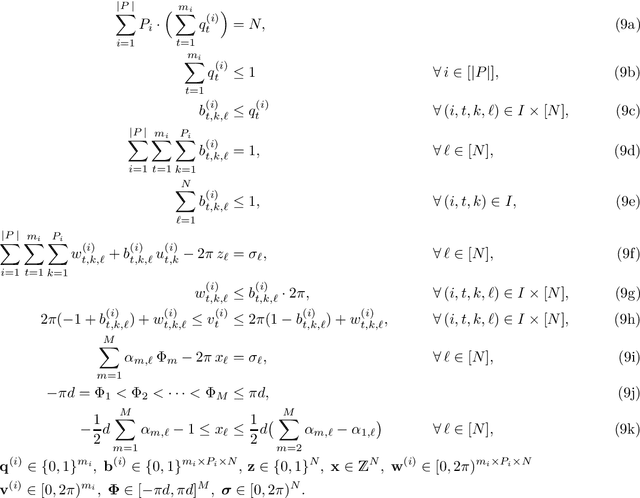
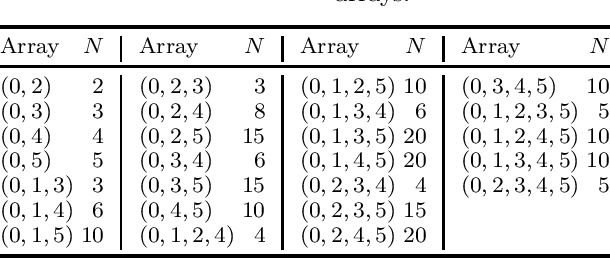
In this paper, we present a novel approach to compute ambiguities in thinned uniform linear arrays, i.e., sparse non-uniform linear arrays, via a mixed-integer program. Ambiguities arise when there exists a set of distinct directions-of-arrival, for which the corresponding steering matrix is rank-deficient and are associated with nonunique parameter estimation. Our approach uses Young tableaux for which a submatrix of the steering matrix has a vanishing determinant, which can be expressed through vanishing sums of unit roots. Each of these vanishing sums then corresponds to an ambiguous set of directions-of-arrival. We derive a method to enumerate such ambiguous sets using a mixed-integer program and present results on several examples.

Successive Convex Approximation for Phase Retrieval with Dictionary Learning

Phase retrieval aims at reconstructing unknown signals from magnitude measurements of linear mixtures. In this paper, we consider the phase retrieval with dictionary learning problem, which includes an additional prior information that the measured signal admits a sparse representation over an unknown dictionary. The task is to jointly estimate the dictionary and the sparse representation from magnitude-only measurements. To this end, we study two complementary formulations and propose efficient parallel algorithms based on the successive convex approximation framework. The first algorithm is termed compact-SCAphase and is preferable in the case of less diverse mixture models. It employs a compact formulation that avoids the use of auxiliary variables. The proposed algorithm is highly scalable and has reduced parameter tuning cost. The second algorithm, referred to as SCAphase, uses auxiliary variables and is favorable in the case of highly diverse mixture models. It also renders simple incorporation of additional side constraints. The performance of both methods is evaluated when applied to blind sparse channel estimation from subband magnitude measurements in a multi-antenna random access network. Simulation results demonstrate the efficiency of the proposed techniques compared to state-of-the-art methods.