Decentralized Eigendecomposition for Online Learning over Graphs with Applications
Paper and Code
Sep 02, 2022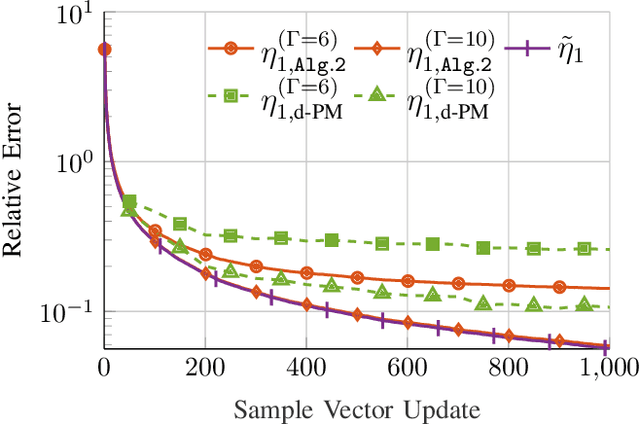
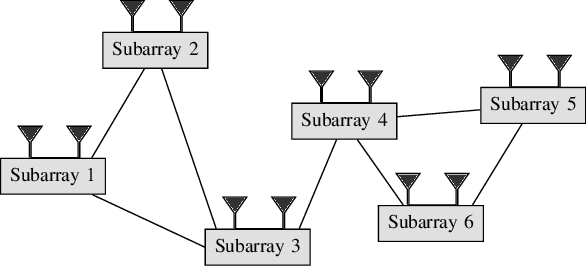
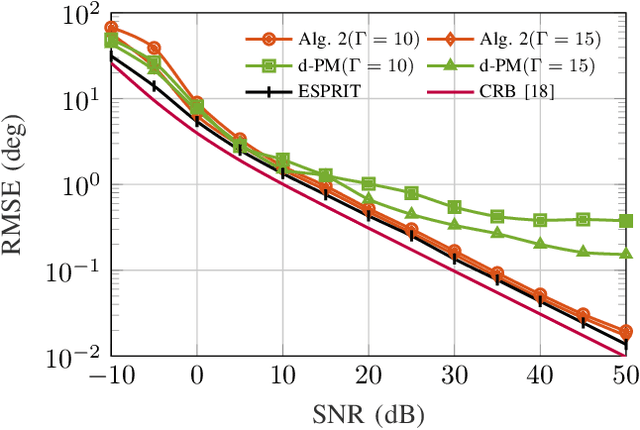
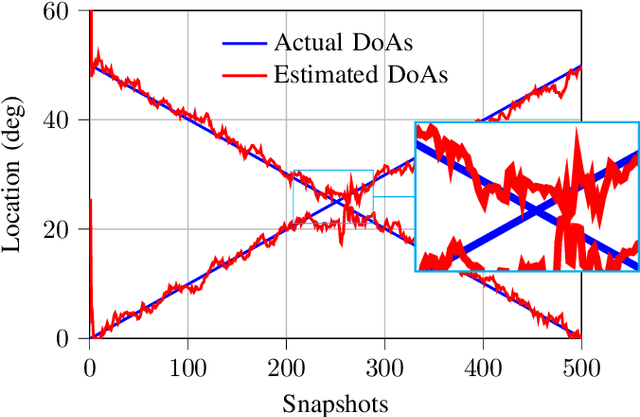
In this paper, the problem of decentralized eigenvalue decomposition of a general symmetric matrix that is important, e.g., in Principal Component Analysis, is studied, and a decentralized online learning algorithm is proposed. Instead of collecting all information in a fusion center, the proposed algorithm involves only local interactions among adjacent agents. It benefits from the representation of the matrix as a sum of rank-one components which makes the algorithm attractive for online eigenvalue and eigenvector tracking applications. We examine the performance of the proposed algorithm in two types of important application examples: First, we consider the online eigendecomposition of a sample covariance matrix over the network, with application in decentralized Direction-of-Arrival (DoA) estimation and DoA tracking applications. Then, we investigate the online computation of the spectra of the graph Laplacian that is important in, e.g., Graph Fourier Analysis and graph dependent filter design. We apply our proposed algorithm to track the spectra of the graph Laplacian in static and dynamic networks. Simulation results reveal that the proposed algorithm outperforms existing decentralized algorithms both in terms of estimation accuracy as well as communication cost.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge