Three more Decades in Array Signal Processing Research: An Optimization and Structure Exploitation Perspective

The signal processing community currently witnesses the emergence of sensor array processing and Direction-of-Arrival (DoA) estimation in various modern applications, such as automotive radar, mobile user and millimeter wave indoor localization, drone surveillance, as well as in new paradigms, such as joint sensing and communication in future wireless systems. This trend is further enhanced by technology leaps and availability of powerful and affordable multi-antenna hardware platforms. The history of advances in super resolution DoA estimation techniques is long, starting from the early parametric multi-source methods such as the computationally expensive maximum likelihood (ML) techniques to the early subspace-based techniques such as Pisarenko and MUSIC. Inspired by the seminal review paper Two Decades of Array Signal Processing Research: The Parametric Approach by Krim and Viberg published in the IEEE Signal Processing Magazine, we are looking back at another three decades in Array Signal Processing Research under the classical narrowband array processing model based on second order statistics. We revisit major trends in the field and retell the story of array signal processing from a modern optimization and structure exploitation perspective. In our overview, through prominent examples, we illustrate how different DoA estimation methods can be cast as optimization problems with side constraints originating from prior knowledge regarding the structure of the measurement system. Due to space limitations, our review of the DoA estimation research in the past three decades is by no means complete. For didactic reasons, we mainly focus on developments in the field that easily relate the traditional multi-source estimation criteria and choose simple illustrative examples.

Decentralized Eigendecomposition for Online Learning over Graphs with Applications

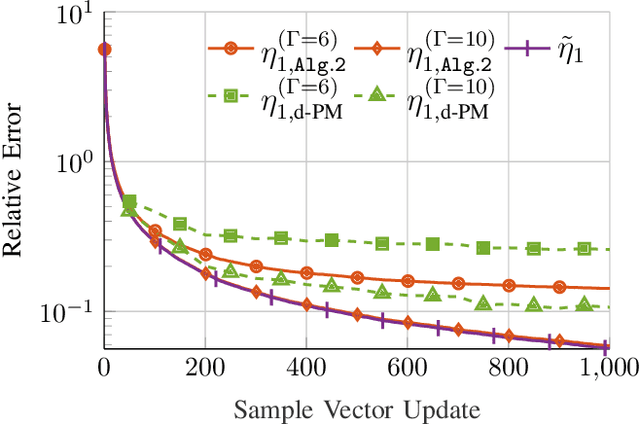
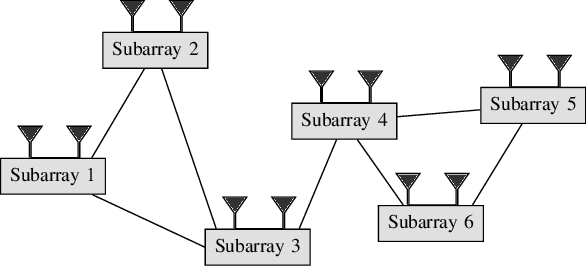
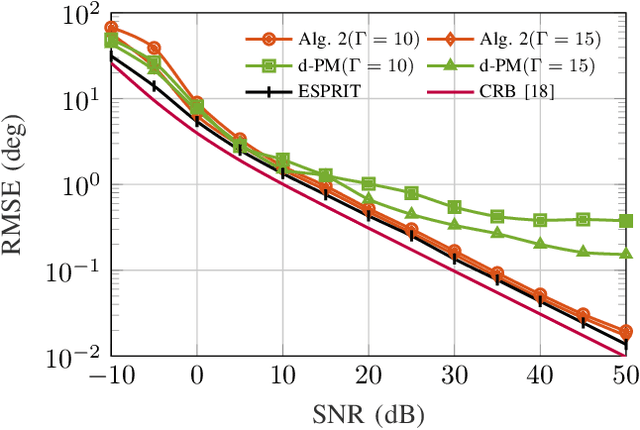
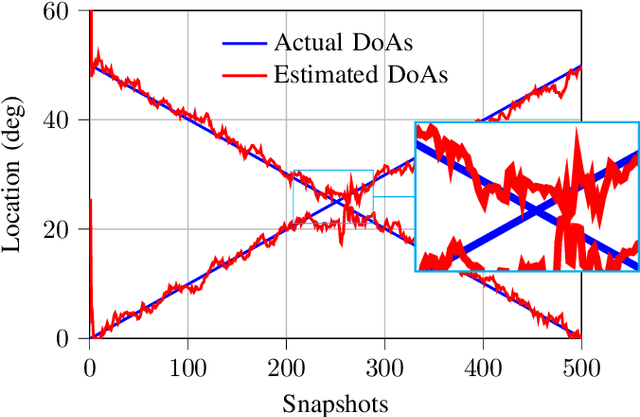
In this paper, the problem of decentralized eigenvalue decomposition of a general symmetric matrix that is important, e.g., in Principal Component Analysis, is studied, and a decentralized online learning algorithm is proposed. Instead of collecting all information in a fusion center, the proposed algorithm involves only local interactions among adjacent agents. It benefits from the representation of the matrix as a sum of rank-one components which makes the algorithm attractive for online eigenvalue and eigenvector tracking applications. We examine the performance of the proposed algorithm in two types of important application examples: First, we consider the online eigendecomposition of a sample covariance matrix over the network, with application in decentralized Direction-of-Arrival (DoA) estimation and DoA tracking applications. Then, we investigate the online computation of the spectra of the graph Laplacian that is important in, e.g., Graph Fourier Analysis and graph dependent filter design. We apply our proposed algorithm to track the spectra of the graph Laplacian in static and dynamic networks. Simulation results reveal that the proposed algorithm outperforms existing decentralized algorithms both in terms of estimation accuracy as well as communication cost.