Cemil Emre Ardic
Integrating AI in NDE: Techniques, Trends, and Further Directions
Apr 04, 2024
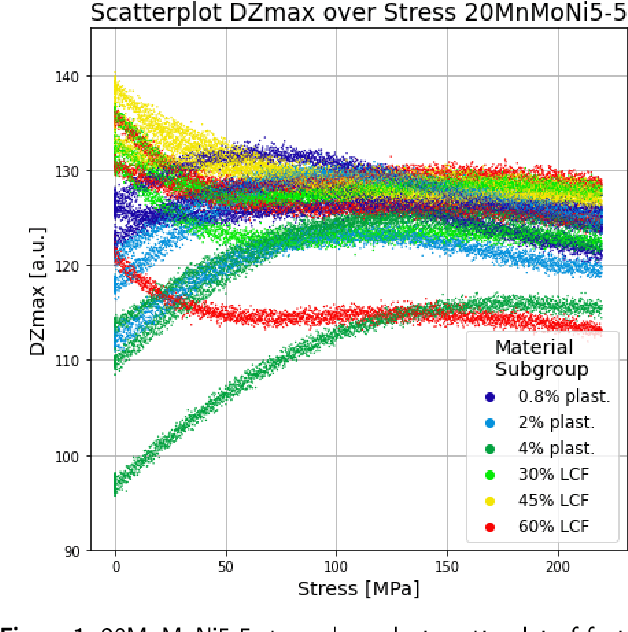
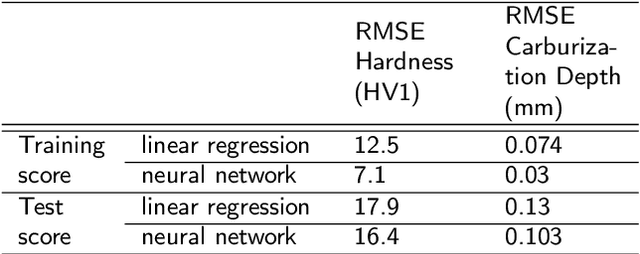
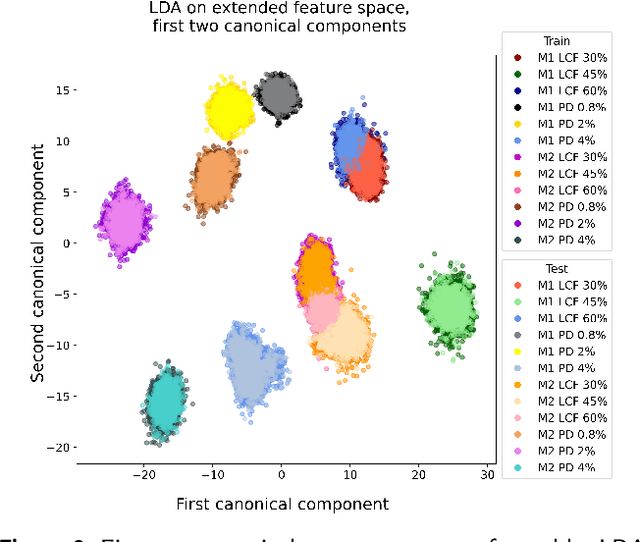
Abstract:The digital transformation is fundamentally changing our industries, affecting planning, execution as well as monitoring of production processes in a wide range of application fields. With product line-ups becoming more and more versatile and diverse, the necessary inspection and monitoring sparks significant novel requirements on the corresponding Nondestructive Evaluation (NDE) systems. The establishment of increasingly powerful approaches to incorporate Artificial Intelligence (AI) may provide just the needed innovation to solve some of these challenges. In this paper we provide a comprehensive survey about the usage of AI methods in NDE in light of the recent innovations towards NDE 4.0. Since we cannot discuss each NDE modality in one paper, we limit our attention to magnetic methods, ultrasound, thermography, as well as optical inspection. In addition to reviewing recent AI developments in each field, we draw common connections by pointing out NDE-related tasks that have a common underlying mathematical problem and categorizing the state of the art according to the corresponding sub-tasks. In so doing, interdisciplinary connections are drawn that provide a more complete overall picture.
Decentralized Eigendecomposition for Online Learning over Graphs with Applications
Sep 02, 2022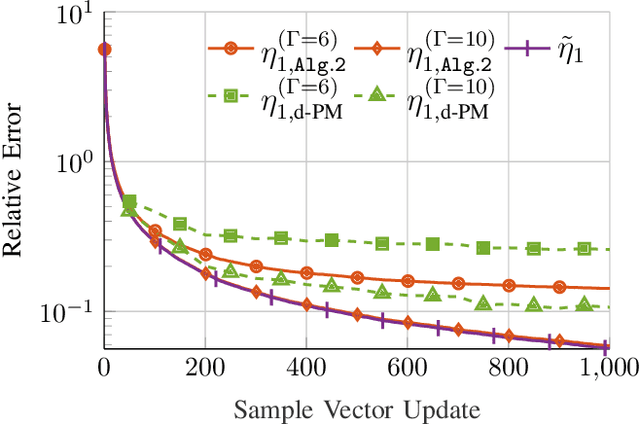
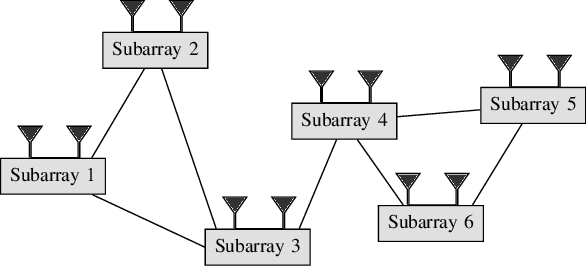
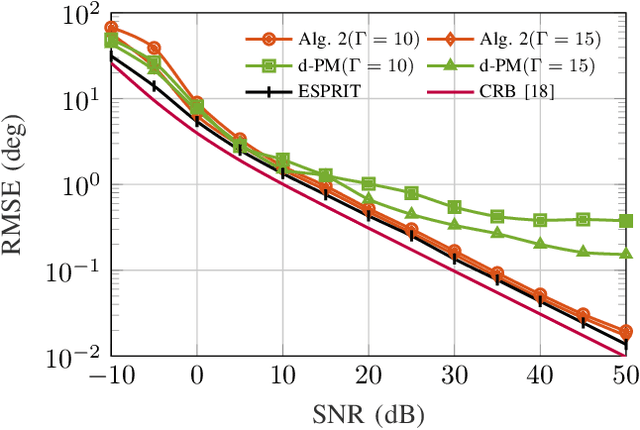
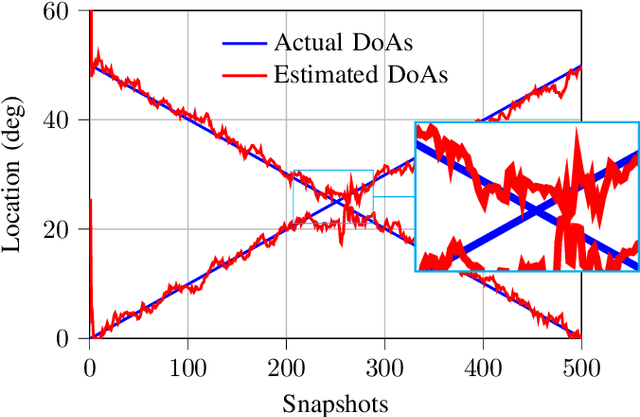
Abstract:In this paper, the problem of decentralized eigenvalue decomposition of a general symmetric matrix that is important, e.g., in Principal Component Analysis, is studied, and a decentralized online learning algorithm is proposed. Instead of collecting all information in a fusion center, the proposed algorithm involves only local interactions among adjacent agents. It benefits from the representation of the matrix as a sum of rank-one components which makes the algorithm attractive for online eigenvalue and eigenvector tracking applications. We examine the performance of the proposed algorithm in two types of important application examples: First, we consider the online eigendecomposition of a sample covariance matrix over the network, with application in decentralized Direction-of-Arrival (DoA) estimation and DoA tracking applications. Then, we investigate the online computation of the spectra of the graph Laplacian that is important in, e.g., Graph Fourier Analysis and graph dependent filter design. We apply our proposed algorithm to track the spectra of the graph Laplacian in static and dynamic networks. Simulation results reveal that the proposed algorithm outperforms existing decentralized algorithms both in terms of estimation accuracy as well as communication cost.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge