Misspecification of Multiple Scattering in Scalar Wave Fields and its Impact in Ultrasound Tomography

In this work, we investigate the localization of targets in the presence of multiple scattering. We focus on the often omitted scenario in which measurement data is affected by multiple scattering, and a simpler model is employed in the estimation. We study the impact of such model mismatch by means of the Misspecified Cram\'er-Rao Bound (MCRB). In numerical simulations inspired by tomographic inspection in ultrasound nondestructive testing, the MCRB is shown to correctly describe the estimation variance of localization parameters under misspecification of the wave propagation model. We provide extensive discussion on the utility of the MCRB in the practical task of verifying whether a chosen misspecified model is suitable for localization based on the properties of the maximum likelihood estimator and the nuanced distinction between bias and parameter space differences. Finally, we highlight that careful interpretation is needed whenever employing the classical CRB in the presence of mismatch through numerical examples based on the Born approximation and other simplified propagation models stemming from it.

Integrating AI in NDE: Techniques, Trends, and Further Directions

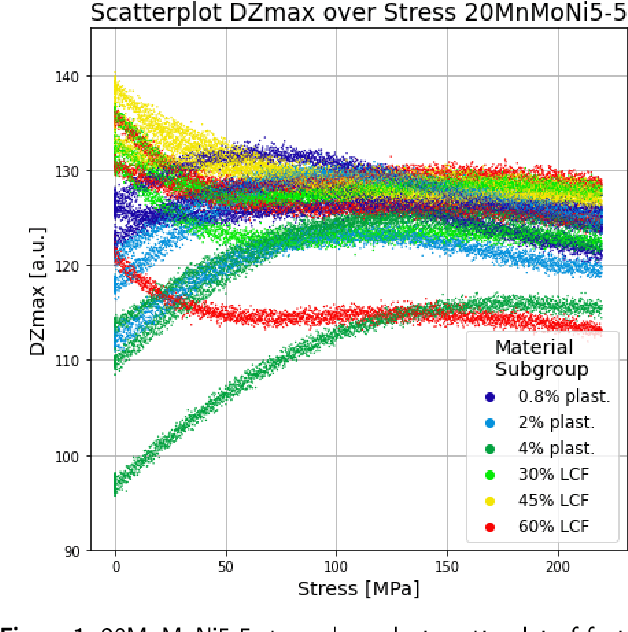
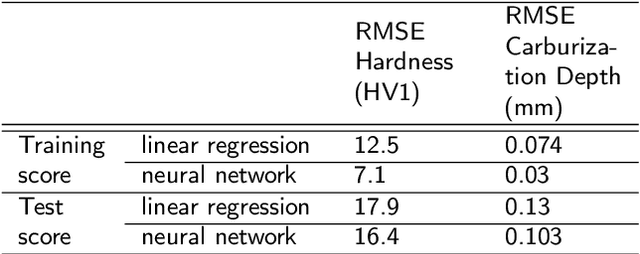
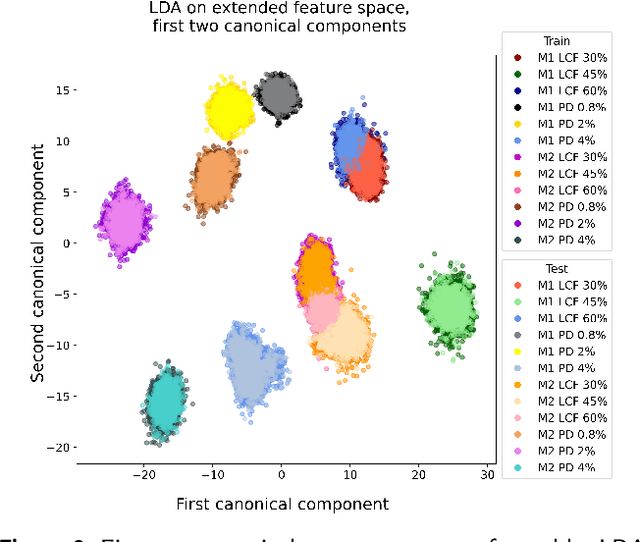
The digital transformation is fundamentally changing our industries, affecting planning, execution as well as monitoring of production processes in a wide range of application fields. With product line-ups becoming more and more versatile and diverse, the necessary inspection and monitoring sparks significant novel requirements on the corresponding Nondestructive Evaluation (NDE) systems. The establishment of increasingly powerful approaches to incorporate Artificial Intelligence (AI) may provide just the needed innovation to solve some of these challenges. In this paper we provide a comprehensive survey about the usage of AI methods in NDE in light of the recent innovations towards NDE 4.0. Since we cannot discuss each NDE modality in one paper, we limit our attention to magnetic methods, ultrasound, thermography, as well as optical inspection. In addition to reviewing recent AI developments in each field, we draw common connections by pointing out NDE-related tasks that have a common underlying mathematical problem and categorizing the state of the art according to the corresponding sub-tasks. In so doing, interdisciplinary connections are drawn that provide a more complete overall picture.