Decentralized Singular Value Decomposition for Extremely Large-scale Antenna Array Systems

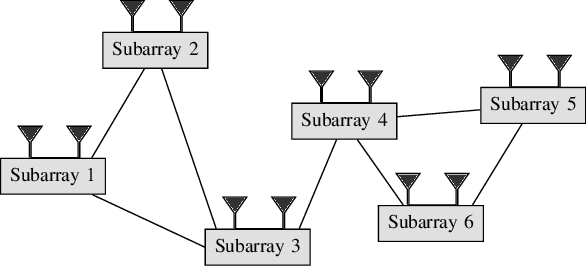
In this article, the problems of decentralized Singular Value Decomposition (d-SVD) and decentralized Principal Component Analysis (d-PCA) are studied, which are fundamental in various signal processing applications. Two scenarios of d-SVD are considered depending on the availability of the data matrix under consideration. In the first scenario, the matrix of interest is row-wisely available in each local node in the network. In the second scenario, the matrix of interest implicitly forms an outer product generated from two different series of measurements. Combining the lightweight local rational function approximation approach and parallel averaging consensus algorithms, two d-SVD algorithms are proposed to cope with the two aforementioned scenarios. We demonstrate the proposed algorithms with two respective application examples for Extremely Large-scale Antenna Array (ELAA) systems: decentralized sensor localization via low-rank matrix completion and decentralized passive radar detection. Moreover, a non-trivial truncation technique, which employs a representative vector that is orthonormal to the principal signal subspace, is proposed to further reduce the associated communication cost with the d-SVD algorithms. Simulation results show that the proposed d-SVD algorithms converge to the centralized solution with reduced communication cost compared to those facilitated with the state-of-the-art decentralized power method.

Decentralized Eigendecomposition for Online Learning over Graphs with Applications

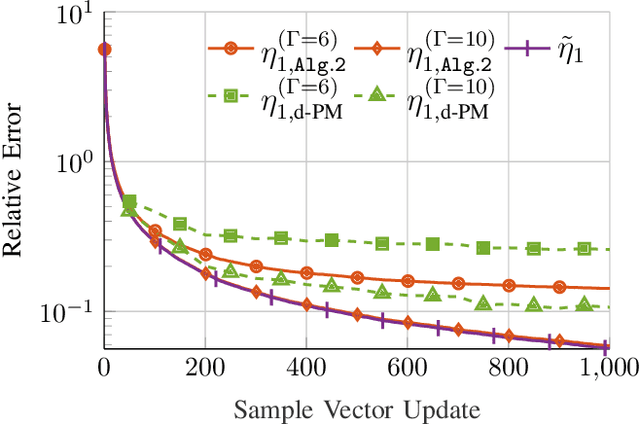
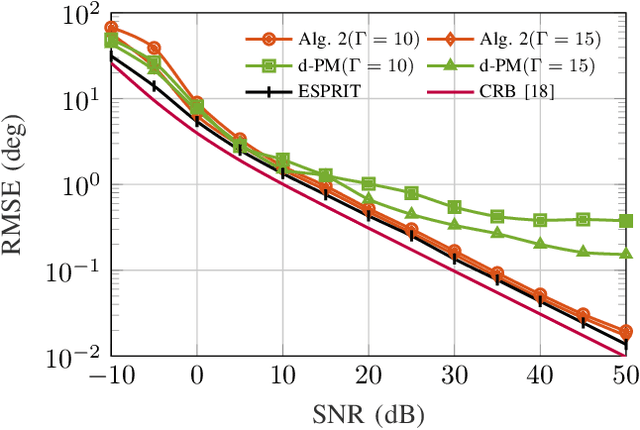
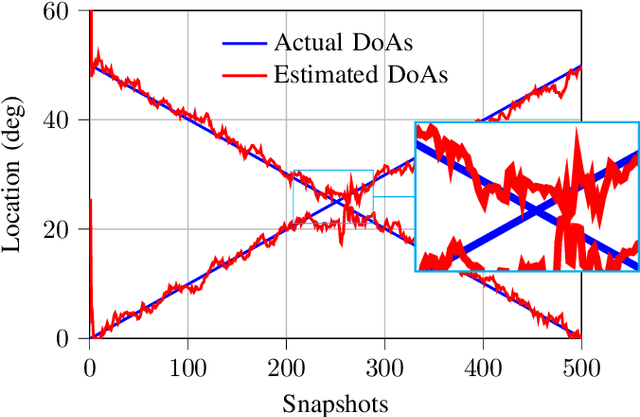
In this paper, the problem of decentralized eigenvalue decomposition of a general symmetric matrix that is important, e.g., in Principal Component Analysis, is studied, and a decentralized online learning algorithm is proposed. Instead of collecting all information in a fusion center, the proposed algorithm involves only local interactions among adjacent agents. It benefits from the representation of the matrix as a sum of rank-one components which makes the algorithm attractive for online eigenvalue and eigenvector tracking applications. We examine the performance of the proposed algorithm in two types of important application examples: First, we consider the online eigendecomposition of a sample covariance matrix over the network, with application in decentralized Direction-of-Arrival (DoA) estimation and DoA tracking applications. Then, we investigate the online computation of the spectra of the graph Laplacian that is important in, e.g., Graph Fourier Analysis and graph dependent filter design. We apply our proposed algorithm to track the spectra of the graph Laplacian in static and dynamic networks. Simulation results reveal that the proposed algorithm outperforms existing decentralized algorithms both in terms of estimation accuracy as well as communication cost.