Ambiguities in Direction-of-Arrival Estimation with Linear Arrays
Paper and Code
Oct 20, 2021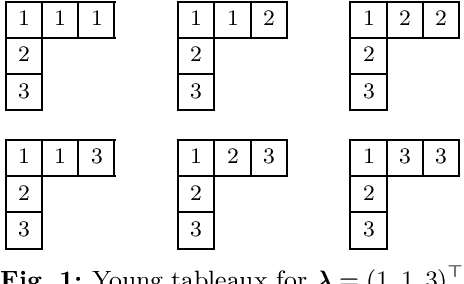
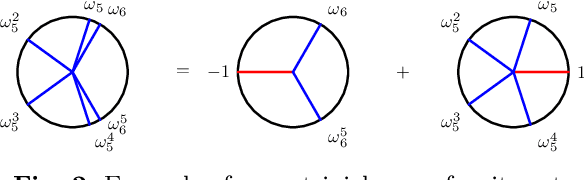
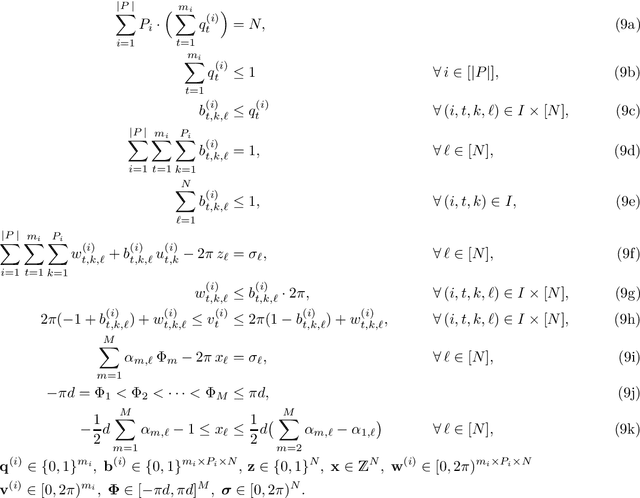
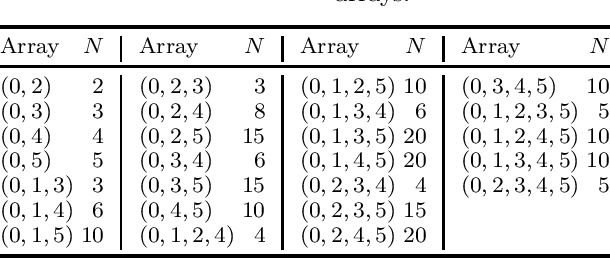
In this paper, we present a novel approach to compute ambiguities in thinned uniform linear arrays, i.e., sparse non-uniform linear arrays, via a mixed-integer program. Ambiguities arise when there exists a set of distinct directions-of-arrival, for which the corresponding steering matrix is rank-deficient and are associated with nonunique parameter estimation. Our approach uses Young tableaux for which a submatrix of the steering matrix has a vanishing determinant, which can be expressed through vanishing sums of unit roots. Each of these vanishing sums then corresponds to an ambiguous set of directions-of-arrival. We derive a method to enumerate such ambiguous sets using a mixed-integer program and present results on several examples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge