Joint Sparse Estimation with Cardinality Constraint via Mixed-Integer Semidefinite Programming

The multiple measurement vectors (MMV) problem refers to the joint estimation of a row-sparse signal matrix from multiple realizations of mixtures with a known dictionary. As a generalization of the standard sparse representation problem for a single measurement, this problem is fundamental in various applications in signal processing, e.g., spectral analysis and direction-of-arrival (DOA) estimation. In this paper, we consider the maximum a posteriori (MAP) estimation for the MMV problem, which is classically formulated as a regularized least-squares (LS) problem with an $\ell_{2,0}$-norm constraint, and derive an equivalent mixed-integer semidefinite program (MISDP) reformulation. The proposed MISDP reformulation can be exactly solved by a generic MISDP solver, which, however, becomes computationally demanding for problems of extremely large dimensions. To further reduce the computation time in such scenarios, a relaxation-based approach can be employed to obtain an approximate solution of the MISDP reformulation, at the expense of a reduced estimation performance. Numerical simulations in the context of DOA estimation demonstrate the improved error performance of our proposed method in comparison to several popular DOA estimation methods. In particular, compared to the deterministic maximum likelihood (DML) estimator, which is often used as a benchmark, the proposed method applied with a state-of-the-art MISDP solver exhibits a superior estimation performance at a significantly reduced running time. Moreover, unlike other nonconvex approaches for the MMV problem, including the greedy methods and the sparse Bayesian learning, the proposed MISDP-based method offers a guarantee of finding a global optimum.

Ambiguities in Direction-of-Arrival Estimation with Linear Arrays

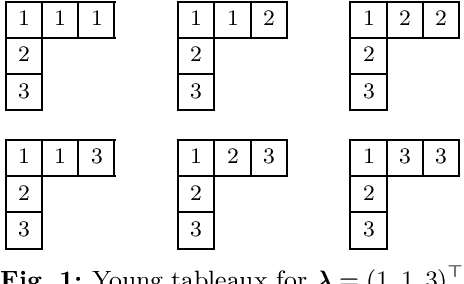
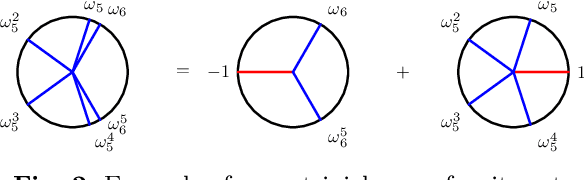
In this paper, we present a novel approach to compute ambiguities in thinned uniform linear arrays, i.e., sparse non-uniform linear arrays, via a mixed-integer program. Ambiguities arise when there exists a set of distinct directions-of-arrival, for which the corresponding steering matrix is rank-deficient and are associated with nonunique parameter estimation. Our approach uses Young tableaux for which a submatrix of the steering matrix has a vanishing determinant, which can be expressed through vanishing sums of unit roots. Each of these vanishing sums then corresponds to an ambiguous set of directions-of-arrival. We derive a method to enumerate such ambiguous sets using a mixed-integer program and present results on several examples.

Recovery under Side Constraints

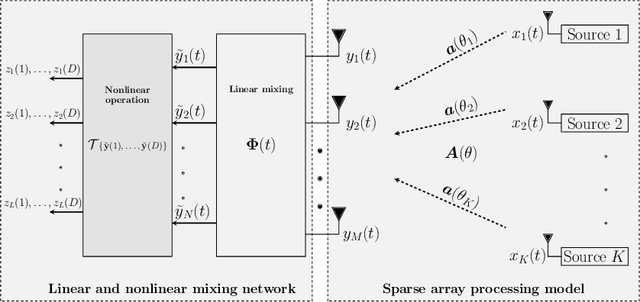
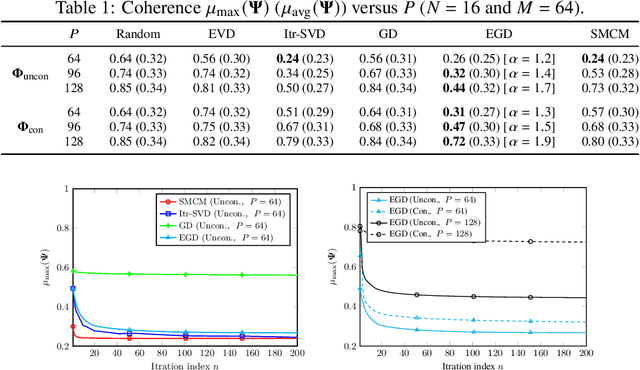
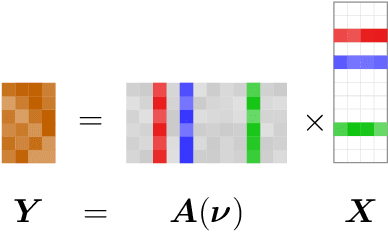
This paper addresses sparse signal reconstruction under various types of structural side constraints with applications in multi-antenna systems. Side constraints may result from prior information on the measurement system and the sparse signal structure. They may involve the structure of the sensing matrix, the structure of the non-zero support values, the temporal structure of the sparse representationvector, and the nonlinear measurement structure. First, we demonstrate how a priori information in form of structural side constraints influence recovery guarantees (null space properties) using L1-minimization. Furthermore, for constant modulus signals, signals with row-, block- and rank-sparsity, as well as non-circular signals, we illustrate how structural prior information can be used to devise efficient algorithms with improved recovery performance and reduced computational complexity. Finally, we address the measurement system design for linear and nonlinear measurements of sparse signals. Moreover, we discuss the linear mixing matrix design based on coherence minimization. Then we extend our focus to nonlinear measurement systems where we design parallel optimization algorithms to efficiently compute stationary points in the sparse phase retrieval problem with and without dictionary learning.