Beyond Spatio-Temporal Representations: Evolving Fourier Transform for Temporal Graphs

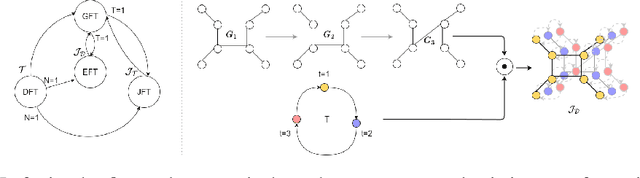
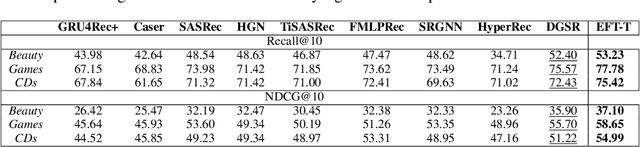
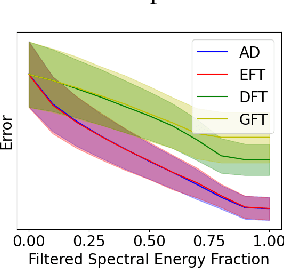
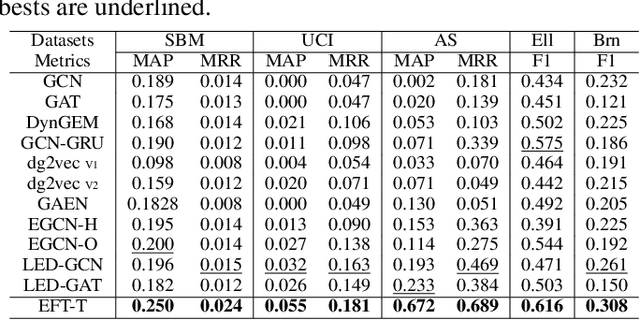
We present the Evolving Graph Fourier Transform (EFT), the first invertible spectral transform that captures evolving representations on temporal graphs. We motivate our work by the inadequacy of existing methods for capturing the evolving graph spectra, which are also computationally expensive due to the temporal aspect along with the graph vertex domain. We view the problem as an optimization over the Laplacian of the continuous time dynamic graph. Additionally, we propose pseudo-spectrum relaxations that decompose the transformation process, making it highly computationally efficient. The EFT method adeptly captures the evolving graph's structural and positional properties, making it effective for downstream tasks on evolving graphs. Hence, as a reference implementation, we develop a simple neural model induced with EFT for capturing evolving graph spectra. We empirically validate our theoretical findings on a number of large-scale and standard temporal graph benchmarks and demonstrate that our model achieves state-of-the-art performance.

Can Persistent Homology provide an efficient alternative for Evaluation of Knowledge Graph Completion Methods?

In this paper we present a novel method, $\textit{Knowledge Persistence}$ ($\mathcal{KP}$), for faster evaluation of Knowledge Graph (KG) completion approaches. Current ranking-based evaluation is quadratic in the size of the KG, leading to long evaluation times and consequently a high carbon footprint. $\mathcal{KP}$ addresses this by representing the topology of the KG completion methods through the lens of topological data analysis, concretely using persistent homology. The characteristics of persistent homology allow $\mathcal{KP}$ to evaluate the quality of the KG completion looking only at a fraction of the data. Experimental results on standard datasets show that the proposed metric is highly correlated with ranking metrics (Hits@N, MR, MRR). Performance evaluation shows that $\mathcal{KP}$ is computationally efficient: In some cases, the evaluation time (validation+test) of a KG completion method has been reduced from 18 hours (using Hits@10) to 27 seconds (using $\mathcal{KP}$), and on average (across methods & data) reduces the evaluation time (validation+test) by $\approx$ $\textbf{99.96}\%$.

Learnable Spectral Wavelets on Dynamic Graphs to Capture Global Interactions

Learning on evolving(dynamic) graphs has caught the attention of researchers as static methods exhibit limited performance in this setting. The existing methods for dynamic graphs learn spatial features by local neighborhood aggregation, which essentially only captures the low pass signals and local interactions. In this work, we go beyond current approaches to incorporate global features for effectively learning representations of a dynamically evolving graph. We propose to do so by capturing the spectrum of the dynamic graph. Since static methods to learn the graph spectrum would not consider the history of the evolution of the spectrum as the graph evolves with time, we propose a novel approach to learn the graph wavelets to capture this evolving spectra. Further, we propose a framework that integrates the dynamically captured spectra in the form of these learnable wavelets into spatial features for incorporating local and global interactions. Experiments on eight standard datasets show that our method significantly outperforms related methods on various tasks for dynamic graphs.

FastGRNN: A Fast, Accurate, Stable and Tiny Kilobyte Sized Gated Recurrent Neural Network

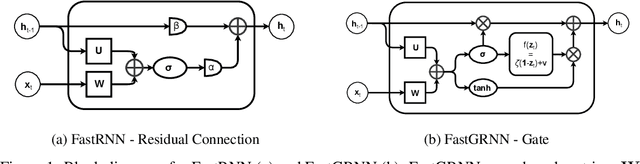
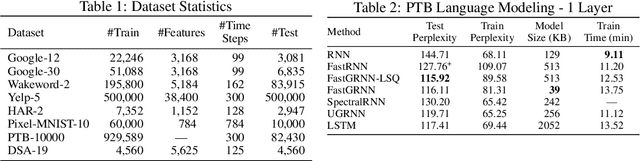
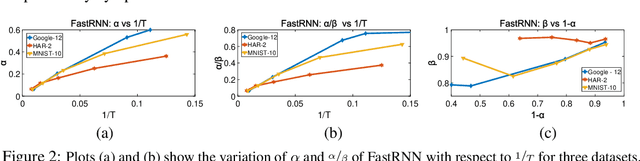
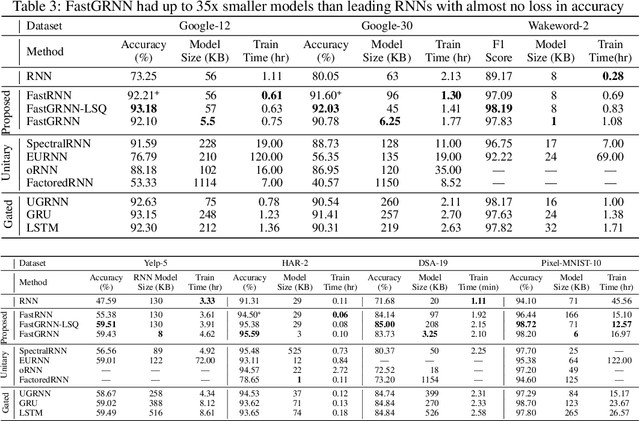
This paper develops the FastRNN and FastGRNN algorithms to address the twin RNN limitations of inaccurate training and inefficient prediction. Previous approaches have improved accuracy at the expense of prediction costs making them infeasible for resource-constrained and real-time applications. Unitary RNNs have increased accuracy somewhat by restricting the range of the state transition matrix's singular values but have also increased the model size as they require a larger number of hidden units to make up for the loss in expressive power. Gated RNNs have obtained state-of-the-art accuracies by adding extra parameters thereby resulting in even larger models. FastRNN addresses these limitations by adding a residual connection that does not constrain the range of the singular values explicitly and has only two extra scalar parameters. FastGRNN then extends the residual connection to a gate by reusing the RNN matrices to match state-of-the-art gated RNN accuracies but with a 2-4x smaller model. Enforcing FastGRNN's matrices to be low-rank, sparse and quantized resulted in accurate models that could be up to 35x smaller than leading gated and unitary RNNs. This allowed FastGRNN to accurately recognize the "Hey Cortana" wakeword with a 1 KB model and to be deployed on severely resource-constrained IoT microcontrollers too tiny to store other RNN models. FastGRNN's code is available at https://github.com/Microsoft/EdgeML/.

Efficient Twitter Sentiment Classification using Subjective Distant Supervision

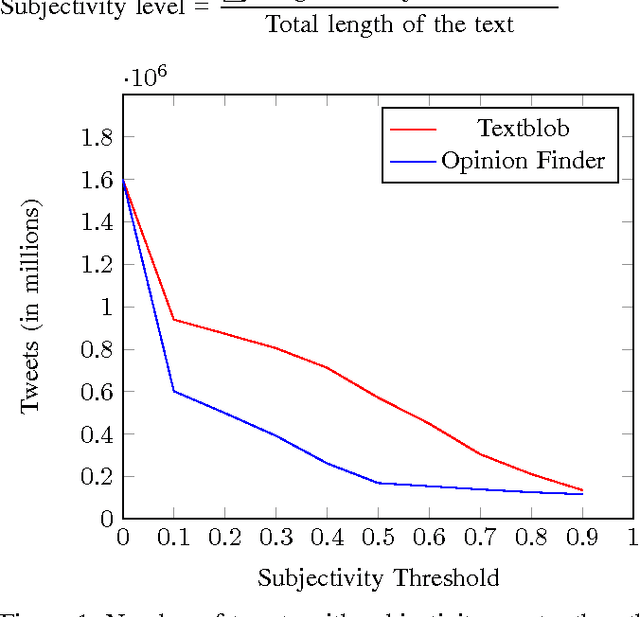
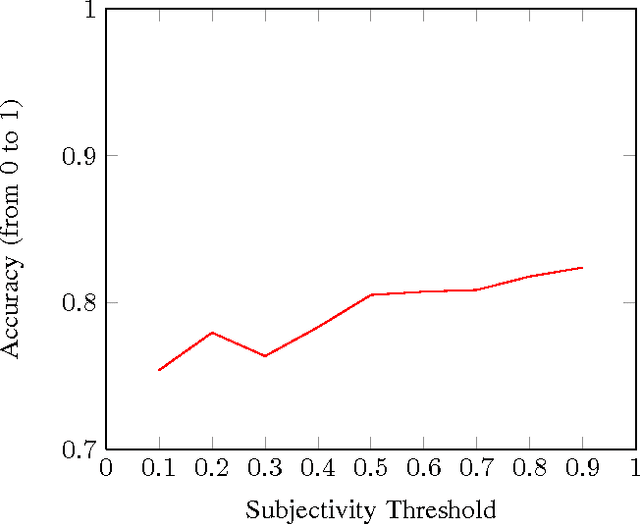
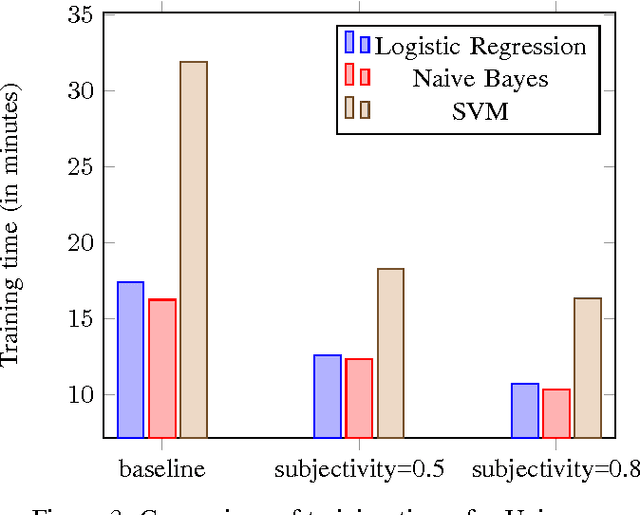
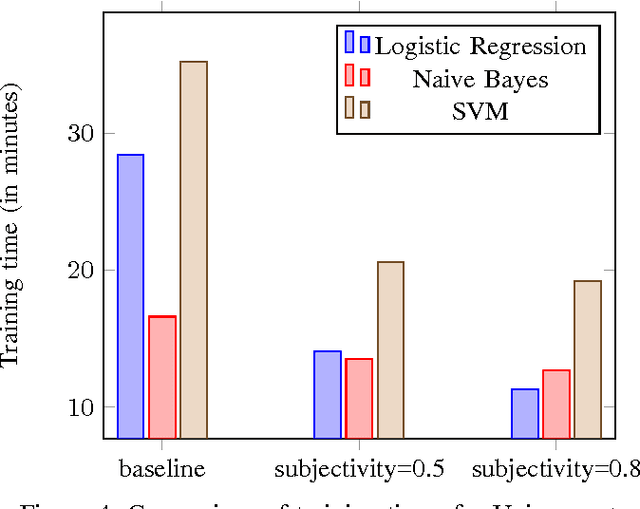
As microblogging services like Twitter are becoming more and more influential in today's globalised world, its facets like sentiment analysis are being extensively studied. We are no longer constrained by our own opinion. Others opinions and sentiments play a huge role in shaping our perspective. In this paper, we build on previous works on Twitter sentiment analysis using Distant Supervision. The existing approach requires huge computation resource for analysing large number of tweets. In this paper, we propose techniques to speed up the computation process for sentiment analysis. We use tweet subjectivity to select the right training samples. We also introduce the concept of EFWS (Effective Word Score) of a tweet that is derived from polarity scores of frequently used words, which is an additional heuristic that can be used to speed up the sentiment classification with standard machine learning algorithms. We performed our experiments using 1.6 million tweets. Experimental evaluations show that our proposed technique is more efficient and has higher accuracy compared to previously proposed methods. We achieve overall accuracies of around 80% (EFWS heuristic gives an accuracy around 85%) on a training dataset of 100K tweets, which is half the size of the dataset used for the baseline model. The accuracy of our proposed model is 2-3% higher than the baseline model, and the model effectively trains at twice the speed of the baseline model.