Beyond Spatio-Temporal Representations: Evolving Fourier Transform for Temporal Graphs
Paper and Code
Feb 25, 2024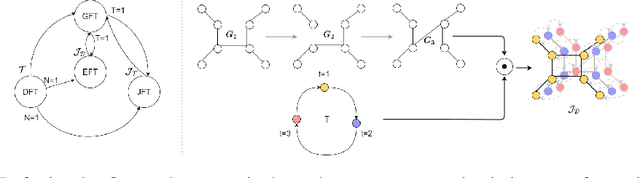
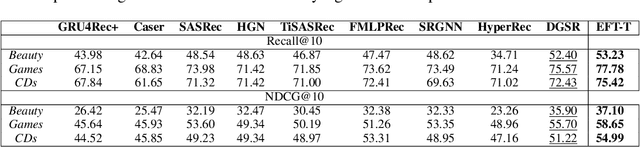
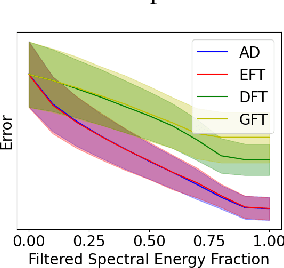
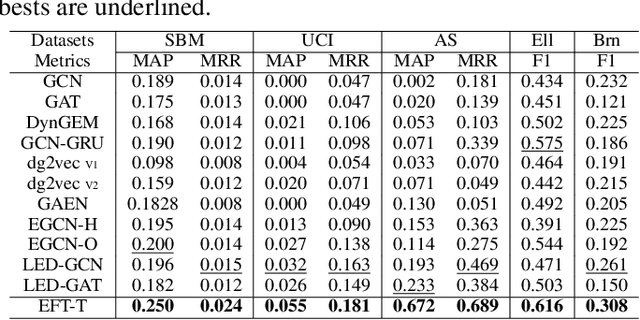
We present the Evolving Graph Fourier Transform (EFT), the first invertible spectral transform that captures evolving representations on temporal graphs. We motivate our work by the inadequacy of existing methods for capturing the evolving graph spectra, which are also computationally expensive due to the temporal aspect along with the graph vertex domain. We view the problem as an optimization over the Laplacian of the continuous time dynamic graph. Additionally, we propose pseudo-spectrum relaxations that decompose the transformation process, making it highly computationally efficient. The EFT method adeptly captures the evolving graph's structural and positional properties, making it effective for downstream tasks on evolving graphs. Hence, as a reference implementation, we develop a simple neural model induced with EFT for capturing evolving graph spectra. We empirically validate our theoretical findings on a number of large-scale and standard temporal graph benchmarks and demonstrate that our model achieves state-of-the-art performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge