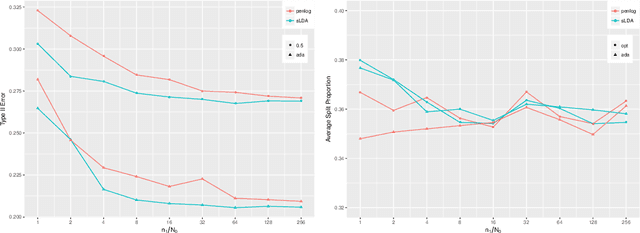
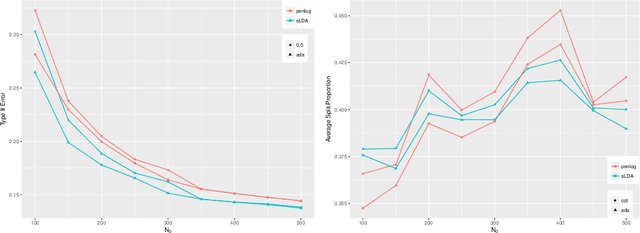
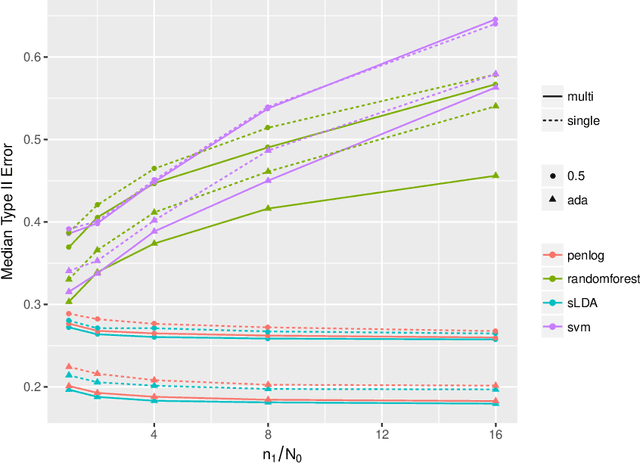
Neyman-Pearson classification: parametrics and power enhancement

The Neyman-Pearson (NP) paradigm in binary classification seeks classifiers that achieve a minimal type II error while enforcing the prioritized type I error under some user-specified level. This paradigm serves naturally in applications such as severe disease diagnosis and spam detection, where people have clear priorities over the two error types. Despite recent advances in NP classification, the NP oracle inequalities, a core theoretical criterion to evaluate classifiers under the NP paradigm, were established only for classifiers based on nonparametric assumptions with bounded feature support. In this work, we conquer the challenges arisen from unbounded feature support in parametric settings and develop NP classification theory and methodology under these settings. Concretely, we propose a new parametric NP classifier NP-sLDA which satisfies the NP oracle inequalities. Furthermore, we construct an adaptive sample splitting scheme that can be applied universally to existing NP classifiers and this adaptive strategy greatly enhances the power of these classifiers. Through extensive numerical experiments and real data studies, we demonstrate the competence of NP-sLDA and the new sample splitting scheme.

Intentional Control of Type I Error over Unconscious Data Distortion: a Neyman-Pearson Approach to Text Classification

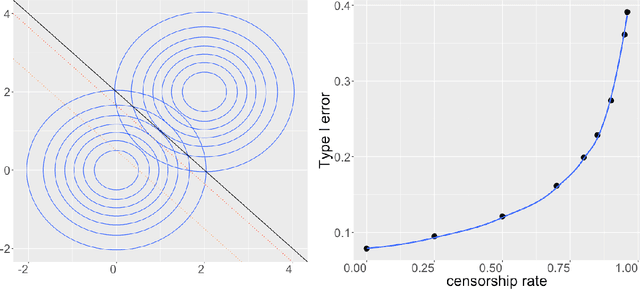
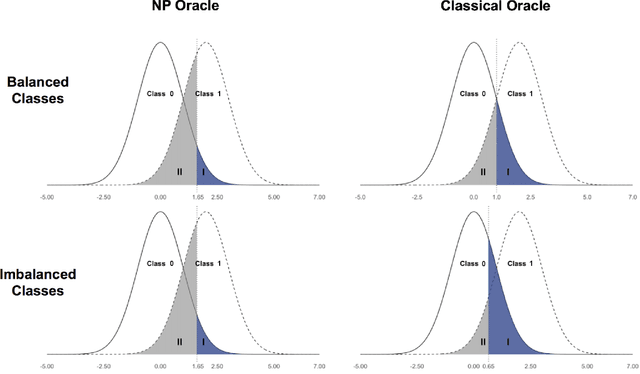
Digital texts have become an increasingly important source of data for social studies. However, textual data from open platforms are vulnerable to manipulation (e.g., censorship and information inflation), often leading to bias in subsequent empirical analysis. This paper investigates the problem of data distortion in text classification when controlling type I error (a relevant textual message is classified as irrelevant) is the priority. The default classical classification paradigm that minimizes the overall classification error can yield an undesirably large type I error, and data distortion exacerbates this situation. As a solution, we propose the Neyman-Pearson (NP) classification paradigm which minimizes type II error under a user-specified type I error constraint. Theoretically, we show that while the classical oracle (i.e., optimal classifier) cannot be recovered under unknown data distortion even if one has the entire post-distortion population, the NP oracle is unaffected by data distortion and can be recovered under the same condition. Empirically, we illustrate the advantage of NP classification methods in a case study that classifies posts about strikes and corruption published on a leading Chinese blogging platform.

A Projection Based Conditional Dependence Measure with Applications to High-dimensional Undirected Graphical Models

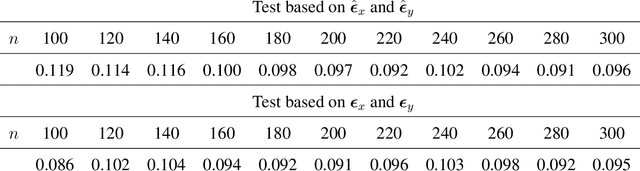
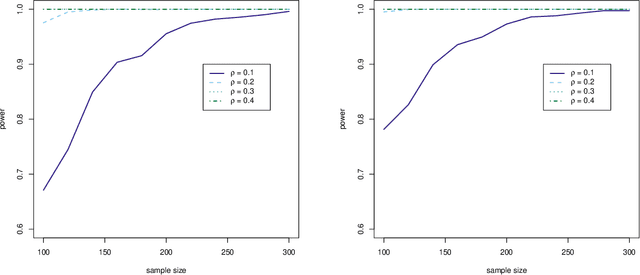
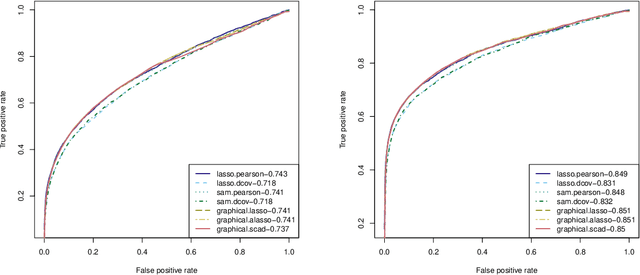
Measuring conditional dependence is an important topic in statistics with broad applications including graphical models. Under a factor model setting, a new conditional dependence measure based on projection is proposed. The corresponding conditional independence test is developed with the asymptotic null distribution unveiled where the number of factors could be high-dimensional. It is also shown that the new test has control over the asymptotic significance level and can be calculated efficiently. A generic method for building dependency graphs without Gaussian assumption using the new test is elaborated. Numerical results and real data analysis show the superiority of the new method.

Aggregation of Affine Estimators

We consider the problem of aggregating a general collection of affine estimators for fixed design regression. Relevant examples include some commonly used statistical estimators such as least squares, ridge and robust least squares estimators. Dalalyan and Salmon (2012) have established that, for this problem, exponentially weighted (EW) model selection aggregation leads to sharp oracle inequalities in expectation, but similar bounds in deviation were not previously known. While results indicate that the same aggregation scheme may not satisfy sharp oracle inequalities with high probability, we prove that a weaker notion of oracle inequality for EW that holds with high probability. Moreover, using a generalization of the newly introduced $Q$-aggregation scheme we also prove sharp oracle inequalities that hold with high probability. Finally, we apply our results to universal aggregation and show that our proposed estimator leads simultaneously to all the best known bounds for aggregation, including $\ell_q$-aggregation, $q \in (0,1)$, with high probability.