Neyman-Pearson classification: parametrics and power enhancement

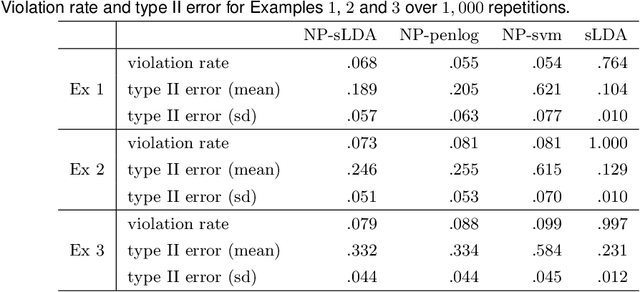
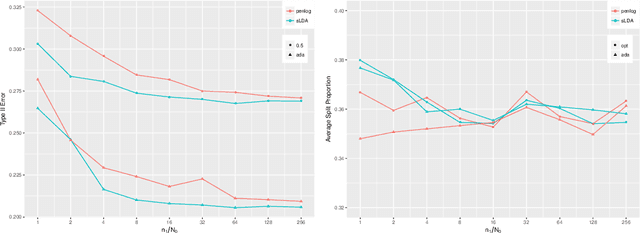
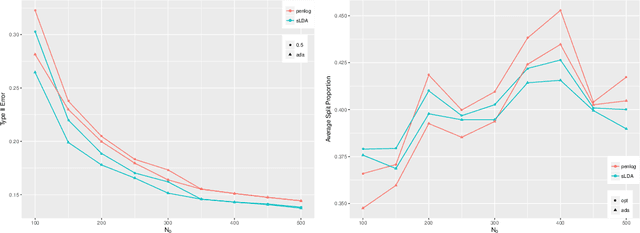
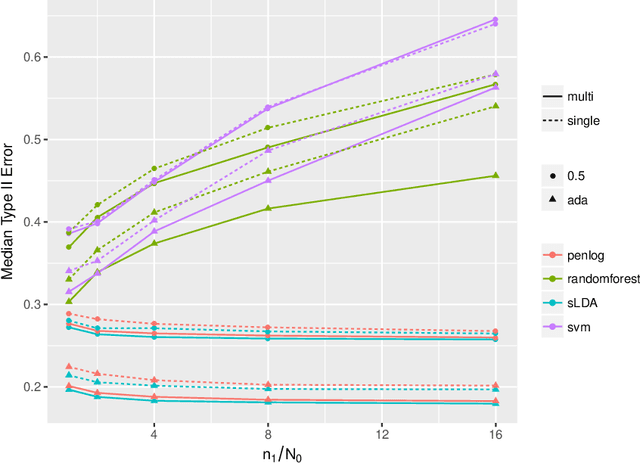
The Neyman-Pearson (NP) paradigm in binary classification seeks classifiers that achieve a minimal type II error while enforcing the prioritized type I error under some user-specified level. This paradigm serves naturally in applications such as severe disease diagnosis and spam detection, where people have clear priorities over the two error types. Despite recent advances in NP classification, the NP oracle inequalities, a core theoretical criterion to evaluate classifiers under the NP paradigm, were established only for classifiers based on nonparametric assumptions with bounded feature support. In this work, we conquer the challenges arisen from unbounded feature support in parametric settings and develop NP classification theory and methodology under these settings. Concretely, we propose a new parametric NP classifier NP-sLDA which satisfies the NP oracle inequalities. Furthermore, we construct an adaptive sample splitting scheme that can be applied universally to existing NP classifiers and this adaptive strategy greatly enhances the power of these classifiers. Through extensive numerical experiments and real data studies, we demonstrate the competence of NP-sLDA and the new sample splitting scheme.