RGB$\leftrightarrow$X: Image decomposition and synthesis using material- and lighting-aware diffusion models

The three areas of realistic forward rendering, per-pixel inverse rendering, and generative image synthesis may seem like separate and unrelated sub-fields of graphics and vision. However, recent work has demonstrated improved estimation of per-pixel intrinsic channels (albedo, roughness, metallicity) based on a diffusion architecture; we call this the RGB$\rightarrow$X problem. We further show that the reverse problem of synthesizing realistic images given intrinsic channels, X$\rightarrow$RGB, can also be addressed in a diffusion framework. Focusing on the image domain of interior scenes, we introduce an improved diffusion model for RGB$\rightarrow$X, which also estimates lighting, as well as the first diffusion X$\rightarrow$RGB model capable of synthesizing realistic images from (full or partial) intrinsic channels. Our X$\rightarrow$RGB model explores a middle ground between traditional rendering and generative models: we can specify only certain appearance properties that should be followed, and give freedom to the model to hallucinate a plausible version of the rest. This flexibility makes it possible to use a mix of heterogeneous training datasets, which differ in the available channels. We use multiple existing datasets and extend them with our own synthetic and real data, resulting in a model capable of extracting scene properties better than previous work and of generating highly realistic images of interior scenes.

Recent Advances in 3D Gaussian Splatting

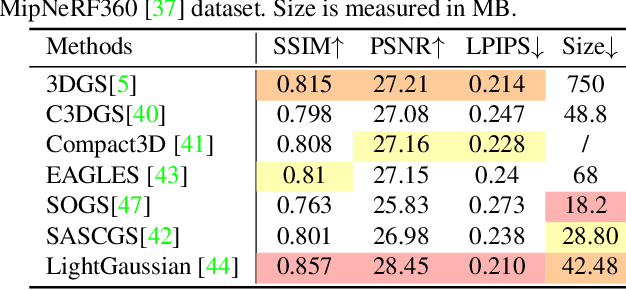
The emergence of 3D Gaussian Splatting (3DGS) has greatly accelerated the rendering speed of novel view synthesis. Unlike neural implicit representations like Neural Radiance Fields (NeRF) that represent a 3D scene with position and viewpoint-conditioned neural networks, 3D Gaussian Splatting utilizes a set of Gaussian ellipsoids to model the scene so that efficient rendering can be accomplished by rasterizing Gaussian ellipsoids into images. Apart from the fast rendering speed, the explicit representation of 3D Gaussian Splatting facilitates editing tasks like dynamic reconstruction, geometry editing, and physical simulation. Considering the rapid change and growing number of works in this field, we present a literature review of recent 3D Gaussian Splatting methods, which can be roughly classified into 3D reconstruction, 3D editing, and other downstream applications by functionality. Traditional point-based rendering methods and the rendering formulation of 3D Gaussian Splatting are also illustrated for a better understanding of this technique. This survey aims to help beginners get into this field quickly and provide experienced researchers with a comprehensive overview, which can stimulate the future development of the 3D Gaussian Splatting representation.

Neural BRDFs: Representation and Operations

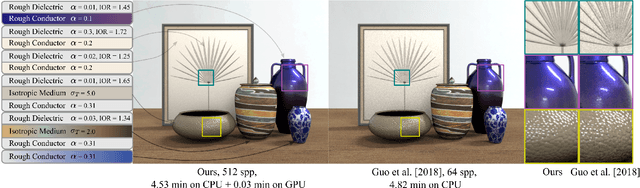
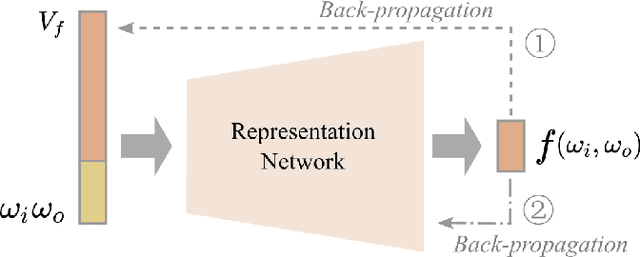
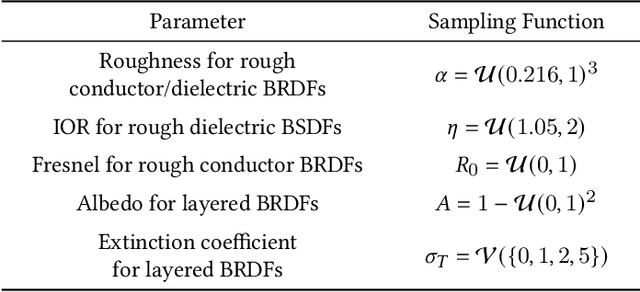
Bidirectional reflectance distribution functions (BRDFs) are pervasively used in computer graphics to produce realistic physically-based appearance. In recent years, several works explored using neural networks to represent BRDFs, taking advantage of neural networks' high compression rate and their ability to fit highly complex functions. However, once represented, the BRDFs will be fixed and therefore lack flexibility to take part in follow-up operations. In this paper, we present a form of "Neural BRDF algebra", and focus on both representation and operations of BRDFs at the same time. We propose a representation neural network to compress BRDFs into latent vectors, which is able to represent BRDFs accurately. We further propose several operations that can be applied solely in the latent space, such as layering and interpolation. Spatial variation is straightforward to achieve by using textures of latent vectors. Furthermore, our representation can be efficiently evaluated and sampled, providing a competitive solution to more expensive Monte Carlo layering approaches.