RNG: Relightable Neural Gaussians

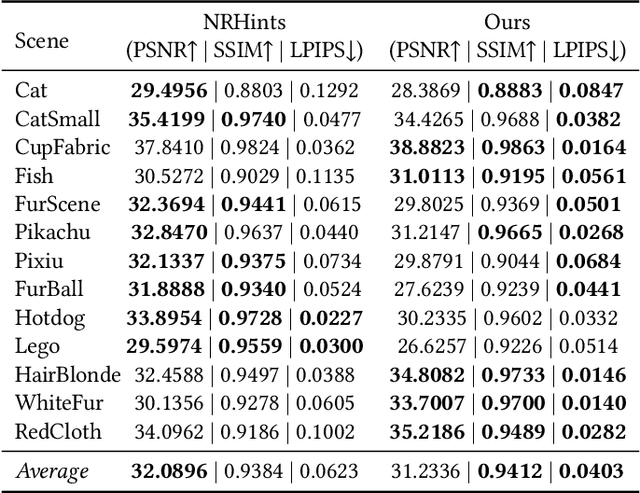
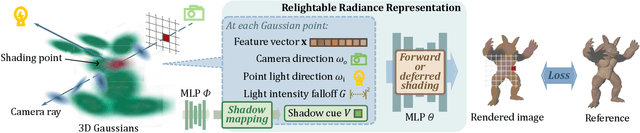
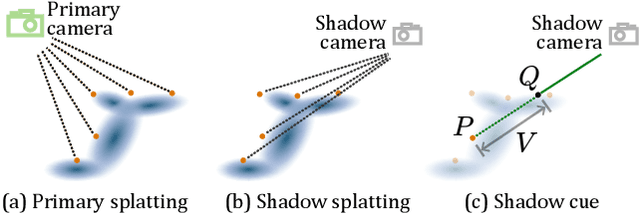
3D Gaussian Splatting (3DGS) has shown its impressive power in novel view synthesis. However, creating relightable 3D assets, especially for objects with ill-defined shapes (e.g., fur), is still a challenging task. For these scenes, the decomposition between the light, geometry, and material is more ambiguous, as neither the surface constraints nor the analytical shading model hold. To address this issue, we propose RNG, a novel representation of relightable neural Gaussians, enabling the relighting of objects with both hard surfaces or fluffy boundaries. We avoid any assumptions in the shading model but maintain feature vectors, which can be further decoded by an MLP into colors, in each Gaussian point. Following prior work, we utilize a point light to reduce the ambiguity and introduce a shadow-aware condition to the network. We additionally propose a depth refinement network to help the shadow computation under the 3DGS framework, leading to better shadow effects under point lights. Furthermore, to avoid the blurriness brought by the alpha-blending in 3DGS, we design a hybrid forward-deferred optimization strategy. As a result, we achieve about $20\times$ faster in training and about $600\times$ faster in rendering than prior work based on neural radiance fields, with $60$ frames per second on an RTX4090.

Neural BRDFs: Representation and Operations

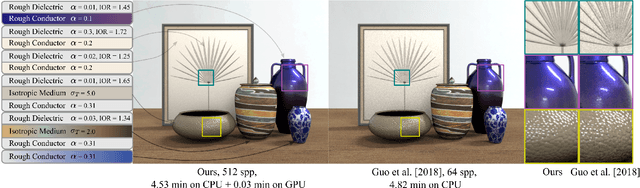
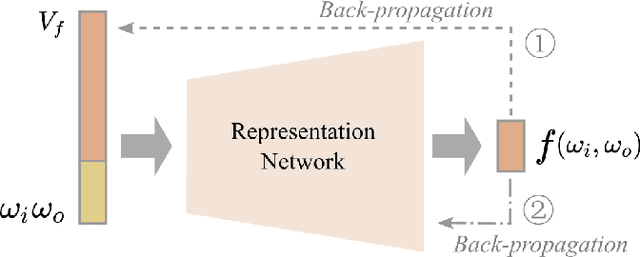
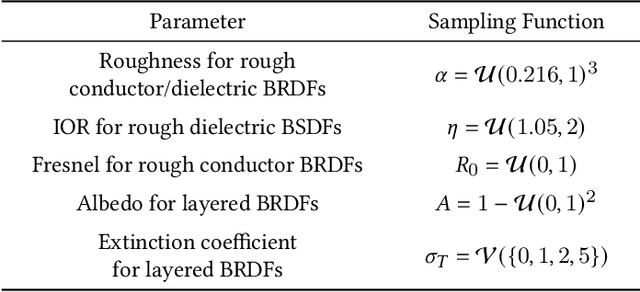
Bidirectional reflectance distribution functions (BRDFs) are pervasively used in computer graphics to produce realistic physically-based appearance. In recent years, several works explored using neural networks to represent BRDFs, taking advantage of neural networks' high compression rate and their ability to fit highly complex functions. However, once represented, the BRDFs will be fixed and therefore lack flexibility to take part in follow-up operations. In this paper, we present a form of "Neural BRDF algebra", and focus on both representation and operations of BRDFs at the same time. We propose a representation neural network to compress BRDFs into latent vectors, which is able to represent BRDFs accurately. We further propose several operations that can be applied solely in the latent space, such as layering and interpolation. Spatial variation is straightforward to achieve by using textures of latent vectors. Furthermore, our representation can be efficiently evaluated and sampled, providing a competitive solution to more expensive Monte Carlo layering approaches.