Ling-Xiao Zhang
Recent Advances in 3D Gaussian Splatting
Mar 17, 2024


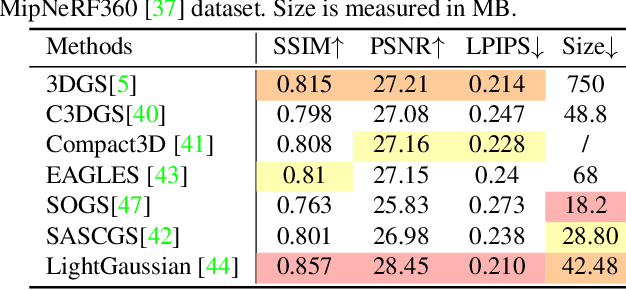
Abstract:The emergence of 3D Gaussian Splatting (3DGS) has greatly accelerated the rendering speed of novel view synthesis. Unlike neural implicit representations like Neural Radiance Fields (NeRF) that represent a 3D scene with position and viewpoint-conditioned neural networks, 3D Gaussian Splatting utilizes a set of Gaussian ellipsoids to model the scene so that efficient rendering can be accomplished by rasterizing Gaussian ellipsoids into images. Apart from the fast rendering speed, the explicit representation of 3D Gaussian Splatting facilitates editing tasks like dynamic reconstruction, geometry editing, and physical simulation. Considering the rapid change and growing number of works in this field, we present a literature review of recent 3D Gaussian Splatting methods, which can be roughly classified into 3D reconstruction, 3D editing, and other downstream applications by functionality. Traditional point-based rendering methods and the rendering formulation of 3D Gaussian Splatting are also illustrated for a better understanding of this technique. This survey aims to help beginners get into this field quickly and provide experienced researchers with a comprehensive overview, which can stimulate the future development of the 3D Gaussian Splatting representation.
High-Fidelity Point Cloud Completion with Low-Resolution Recovery and Noise-Aware Upsampling
Dec 22, 2021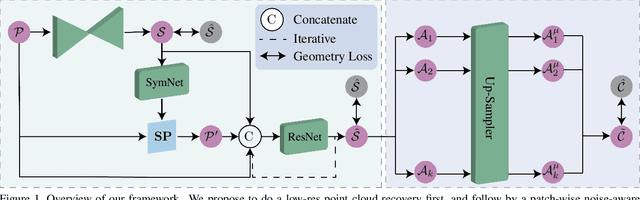
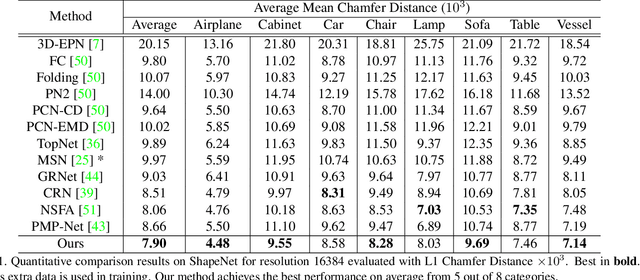
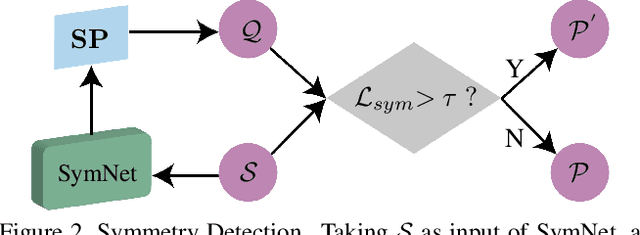
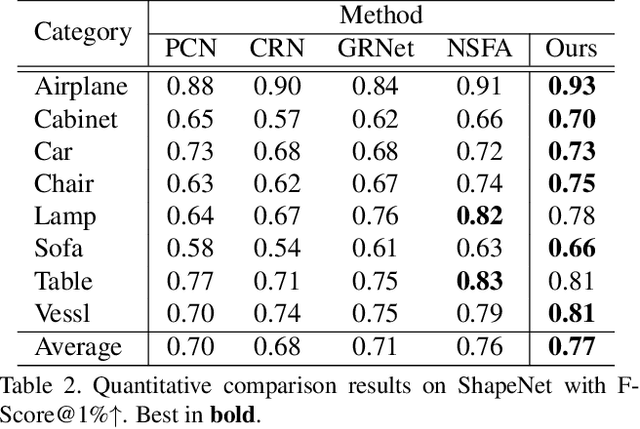
Abstract:Completing an unordered partial point cloud is a challenging task. Existing approaches that rely on decoding a latent feature to recover the complete shape, often lead to the completed point cloud being over-smoothing, losing details, and noisy. Instead of decoding a whole shape, we propose to decode and refine a low-resolution (low-res) point cloud first, and then performs a patch-wise noise-aware upsampling rather than interpolating the whole sparse point cloud at once, which tends to lose details. Regarding the possibility of lacking details of the initially decoded low-res point cloud, we propose an iterative refinement to recover the geometric details and a symmetrization process to preserve the trustworthy information from the input partial point cloud. After obtaining a sparse and complete point cloud, we propose a patch-wise upsampling strategy. Patch-based upsampling allows to better recover fine details unlike decoding a whole shape, however, the existing upsampling methods are not applicable to completion task due to the data discrepancy (i.e., input sparse data here is not from ground-truth). Therefore, we propose a patch extraction approach to generate training patch pairs between the sparse and ground-truth point clouds, and an outlier removal step to suppress the noisy points from the sparse point cloud. Together with the low-res recovery, our whole method is able to achieve high-fidelity point cloud completion. Comprehensive evaluations are provided to demonstrate the effectiveness of the proposed method and its individual components.
PRS-Net: Planar Reflective Symmetry Detection Net for 3D Models
Oct 24, 2019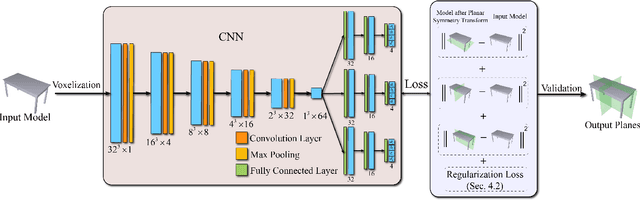

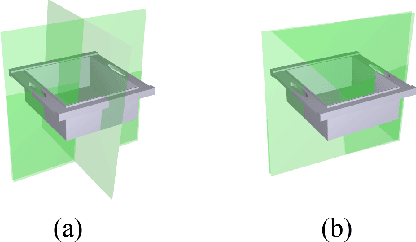

Abstract:In geometry processing, symmetry is the universally high-level structural information of the 3d models and benefits many geometry processing tasks including shape segmentation, alignment, matching, completion, e.g.. Thus it is an important problem to analyze various forms of the symmetry of 3D shapes. The planar reflective symmetry is the most fundamental one. Traditional methods based on spatial sampling can be time consuming and may not be able to identify all the symmetry planes. In this paper, we present a novel learning framework to automatically discover global planar reflective symmetry of a 3D shape. Our framework trains an unsupervised 3D convolutional neural network to extract global model features and then outputs possible global symmetry parameters, where input shapes are represented using voxels. We introduce a dedicated symmetry distance loss along with a regularization loss to avoid generating duplicated symmetry planes. Our network can also identify isotropic shapes by predicting their rotation axes. We further provide a method to remove invalid and duplicated planes and axes. We demonstrate that our method is able to produce reliable and accurate results. Our neural network-based method is hundreds of times faster than the state-of-the-art method, which is based on sampling. Our method is also robust even with noisy or incomplete input surfaces.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge