Point-based Acoustic Scattering for Interactive Sound Propagation via Surface Encoding

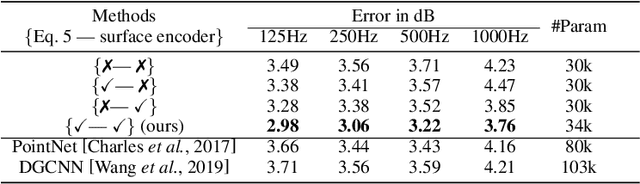
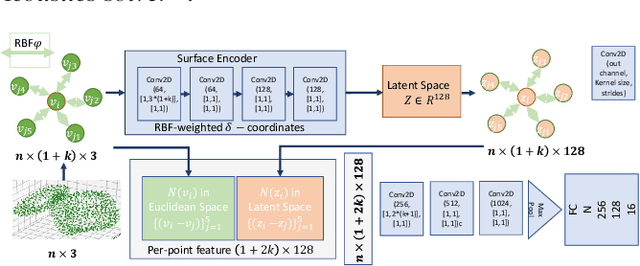
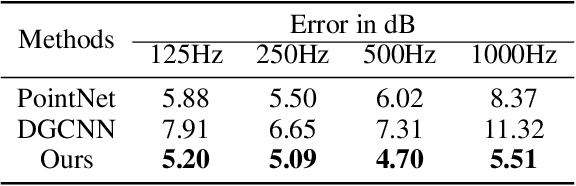
We present a novel geometric deep learning method to compute the acoustic scattering properties of geometric objects. Our learning algorithm uses a point cloud representation of objects to compute the scattering properties and integrates them with ray tracing for interactive sound propagation in dynamic scenes. We use discrete Laplacian-based surface encoders and approximate the neighborhood of each point using a shared multi-layer perceptron. We show that our formulation is permutation invariant and present a neural network that computes the scattering function using spherical harmonics. Our approach can handle objects with arbitrary topologies and deforming models, and takes less than 1ms per object on a commodity GPU. We have analyzed the accuracy and perform validation on thousands of unseen 3D objects and highlight the benefits over other point-based geometric deep learning methods. To the best of our knowledge, this is the first real-time learning algorithm that can approximate the acoustic scattering properties of arbitrary objects with high accuracy.

PRS-Net: Planar Reflective Symmetry Detection Net for 3D Models

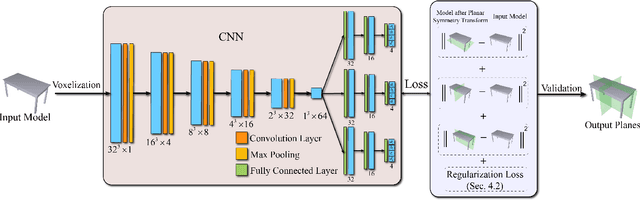
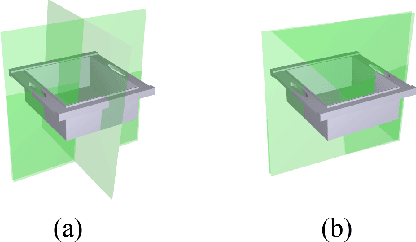
In geometry processing, symmetry is the universally high-level structural information of the 3d models and benefits many geometry processing tasks including shape segmentation, alignment, matching, completion, e.g.. Thus it is an important problem to analyze various forms of the symmetry of 3D shapes. The planar reflective symmetry is the most fundamental one. Traditional methods based on spatial sampling can be time consuming and may not be able to identify all the symmetry planes. In this paper, we present a novel learning framework to automatically discover global planar reflective symmetry of a 3D shape. Our framework trains an unsupervised 3D convolutional neural network to extract global model features and then outputs possible global symmetry parameters, where input shapes are represented using voxels. We introduce a dedicated symmetry distance loss along with a regularization loss to avoid generating duplicated symmetry planes. Our network can also identify isotropic shapes by predicting their rotation axes. We further provide a method to remove invalid and duplicated planes and axes. We demonstrate that our method is able to produce reliable and accurate results. Our neural network-based method is hundreds of times faster than the state-of-the-art method, which is based on sampling. Our method is also robust even with noisy or incomplete input surfaces.