FISTA Iterates Converge Linearly for Denoiser-Driven Regularization

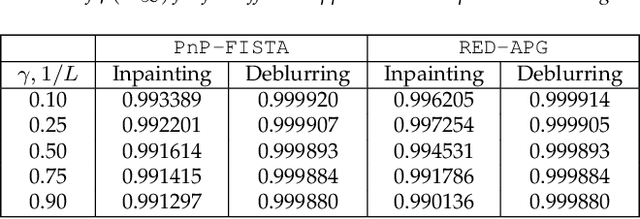
The effectiveness of denoising-driven regularization for image reconstruction has been widely recognized. Two prominent algorithms in this area are Plug-and-Play ($\texttt{PnP}$) and Regularization-by-Denoising ($\texttt{RED}$). We consider two specific algorithms $\texttt{PnP-FISTA}$ and $\texttt{RED-APG}$, where regularization is performed by replacing the proximal operator in the $\texttt{FISTA}$ algorithm with a powerful denoiser. The iterate convergence of $\texttt{FISTA}$ is known to be challenging with no universal guarantees. Yet, we show that for linear inverse problems and a class of linear denoisers, global linear convergence of the iterates of $\texttt{PnP-FISTA}$ and $\texttt{RED-APG}$ can be established through simple spectral analysis.

On the Contractivity of Plug-and-Play Operators

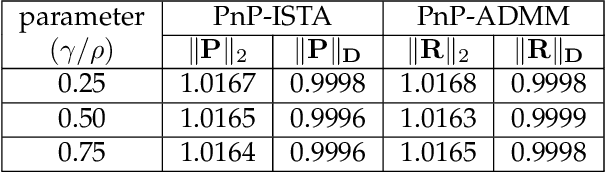
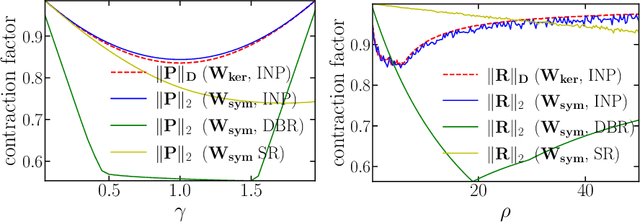
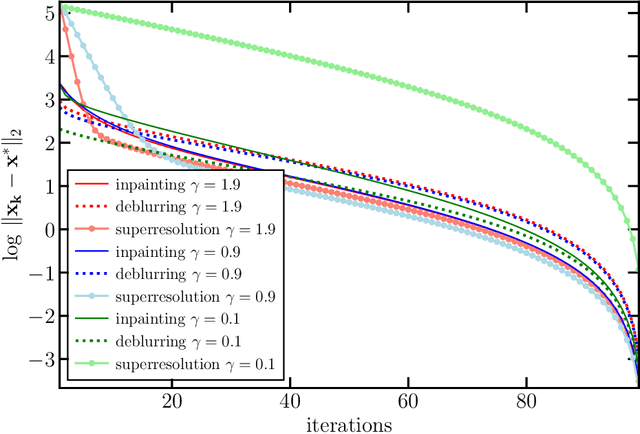
In plug-and-play (PnP) regularization, the proximal operator in algorithms such as ISTA and ADMM is replaced by a powerful denoiser. This formal substitution works surprisingly well in practice. In fact, PnP has been shown to give state-of-the-art results for various imaging applications. The empirical success of PnP has motivated researchers to understand its theoretical underpinnings and, in particular, its convergence. It was shown in prior work that for kernel denoisers such as the nonlocal means, PnP-ISTA provably converges under some strong assumptions on the forward model. The present work is motivated by the following questions: Can we relax the assumptions on the forward model? Can the convergence analysis be extended to PnP-ADMM? Can we estimate the convergence rate? In this letter, we resolve these questions using the contraction mapping theorem: (i) for symmetric denoisers, we show that (under mild conditions) PnP-ISTA and PnP-ADMM exhibit linear convergence; and (ii) for kernel denoisers, we show that PnP-ISTA and PnP-ADMM converge linearly for image inpainting. We validate our theoretical findings using reconstruction experiments.

Guided Nonlocal Patch Regularization and Efficient Filtering-Based Inversion for Multiband Fusion

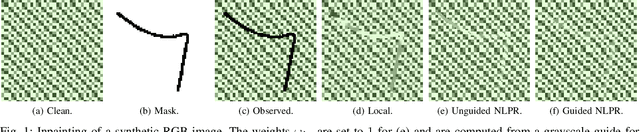
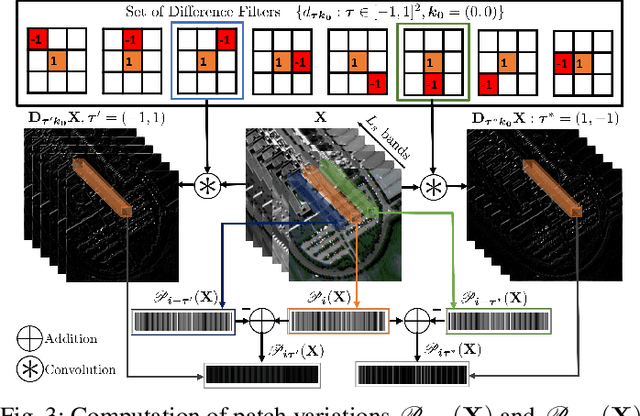
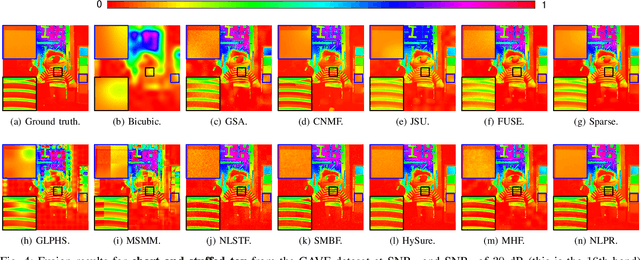
In multiband fusion, an image with a high spatial and low spectral resolution is combined with an image with a low spatial but high spectral resolution to produce a single multiband image having high spatial and spectral resolutions. This comes up in remote sensing applications such as pansharpening~(MS+PAN), hyperspectral sharpening~(HS+PAN), and HS-MS fusion~(HS+MS). Remote sensing images are textured and have repetitive structures. Motivated by nonlocal patch-based methods for image restoration, we propose a convex regularizer that (i) takes into account long-distance correlations, (ii) penalizes patch variation, which is more effective than pixel variation for capturing texture information, and (iii) uses the higher spatial resolution image as a guide image for weight computation. We come up with an efficient ADMM algorithm for optimizing the regularizer along with a standard least-squares loss function derived from the imaging model. The novelty of our algorithm is that by expressing patch variation as filtering operations and by judiciously splitting the original variables and introducing latent variables, we are able to solve the ADMM subproblems efficiently using FFT-based convolution and soft-thresholding. As far as the reconstruction quality is concerned, our method is shown to outperform state-of-the-art variational and deep learning techniques.

Plug-and-Play Regularization using Linear Solvers

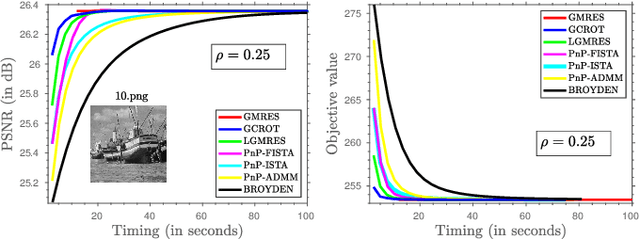
There has been tremendous research on the design of image regularizers over the years, from simple Tikhonov and Laplacian to sophisticated sparsity and CNN-based regularizers. Coupled with a model-based loss function, these are typically used for image reconstruction within an optimization framework. The technical challenge is to develop a regularizer that can accurately model realistic images and be optimized efficiently along with the loss function. Motivated by the recent plug-and-play paradigm for image regularization, we construct a quadratic regularizer whose reconstruction capability is competitive with state-of-the-art regularizers. The novelty of the regularizer is that, unlike classical regularizers, the quadratic objective function is derived from the observed data. Since the regularizer is quadratic, we can reduce the optimization to solving a linear system for applications such as superresolution, deblurring, inpainting, etc. In particular, we show that using iterative Krylov solvers, we can converge to the solution in a few iterations, where each iteration requires an application of the forward operator and a linear denoiser. The surprising finding is that we can get close to deep learning methods in terms of reconstruction quality. To the best of our knowledge, the possibility of achieving near state-of-the-art performance using a linear solver is novel.

Plug-and-Play Compressed Sensing: Theoretical Guarantees on Exact and Robust Recovery

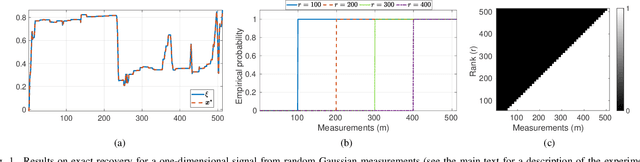
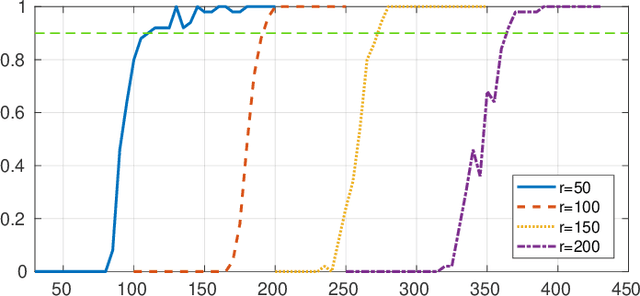
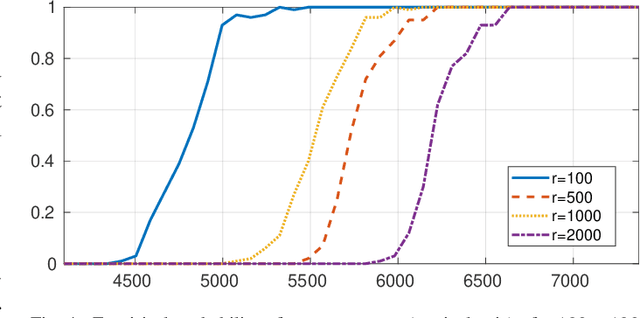
In Plug-and-Play (PnP) algorithms, an off-the-shelf denoiser is used for image regularization. PnP yields state-of-the-art results, but its theoretical aspects are not well understood. This work considers the question: Similar to classical compressed sensing (CS), can we theoretically recover the ground-truth via PnP under suitable conditions on the denoiser and the sensing matrix? One hurdle is that since PnP is an algorithmic framework, its solution need not be the minimizer of some objective function. It was recently shown that a convex regularizer $\Phi$ can be associated with a class of linear denoisers such that PnP amounts to solving a convex problem involving $\Phi$. Motivated by this, we consider the PnP analog of CS: minimize $\Phi(x)$ s.t. $Ax=A\xi$, where $A$ is a $m\times n$ random sensing matrix, $\Phi$ is the regularizer associated with a linear denoiser $W$, and $\xi$ is the ground-truth. We prove that if $A$ is Gaussian and $\xi$ is in the range of $W$, then the minimizer is almost surely $\xi$ if $rank(W)\leq m$, and almost never if $rank(W)> m$. Thus, the range of the PnP denoiser acts as a signal prior, and its dimension marks a sharp transition from failure to success of exact recovery. We extend the result to subgaussian sensing matrices, except that exact recovery holds only with high probability. For noisy measurements $b = A \xi + \eta$, we consider a robust formulation: minimize $\Phi(x)$ s.t. $\|Ax-b\|\leq\delta$. We prove that for an optimal solution $x^*$, with high probability the distortion $\|x^*-\xi\|$ is bounded by $\|\eta\|$ and $\delta$ if the number of measurements is large enough. In particular, we can derive the sample complexity of CS as a function of distortion error and success rate. We discuss the extension of these results to random Fourier measurements, perform numerical experiments, and discuss research directions stemming from this work.

On the Construction of Averaged Deep Denoisers for Image Regularization

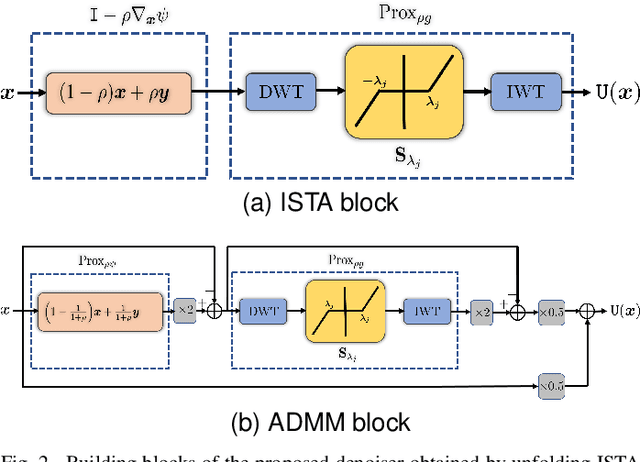
Plug-and-Play (PnP) and Regularization by Denoising (RED) are recent paradigms for image reconstruction that can leverage the power of modern denoisers for image regularization. In particular, these algorithms have been shown to deliver state-of-the-art reconstructions using CNN denoisers. Since the regularization is performed in an ad-hoc manner in PnP and RED, understanding their convergence has been an active research area. Recently, it was observed in many works that iterate convergence of PnP and RED can be guaranteed if the denoiser is averaged or nonexpansive. However, integrating nonexpansivity with gradient-based learning is a challenging task -- checking nonexpansivity is known to be computationally intractable. Using numerical examples, we show that existing CNN denoisers violate the nonexpansive property and can cause the PnP iterations to diverge. In fact, algorithms for training nonexpansive denoisers either cannot guarantee nonexpansivity of the final denoiser or are computationally intensive. In this work, we propose to construct averaged (contractive) image denoisers by unfolding ISTA and ADMM iterations applied to wavelet denoising and demonstrate that their regularization capacity for PnP and RED can be matched with CNN denoisers. To the best of our knowledge, this is the first work to propose a simple framework for training provably averaged (contractive) denoisers using unfolding networks.

On Plug-and-Play Regularization using Linear Denoisers

In plug-and-play (PnP) regularization, the knowledge of the forward model is combined with a powerful denoiser to obtain state-of-the-art image reconstructions. This is typically done by taking a proximal algorithm such as FISTA or ADMM, and formally replacing the proximal map associated with a regularizer by nonlocal means, BM3D or a CNN denoiser. Each iterate of the resulting PnP algorithm involves some kind of inversion of the forward model followed by denoiser-induced regularization. A natural question in this regard is that of optimality, namely, do the PnP iterations minimize some f+g, where f is a loss function associated with the forward model and g is a regularizer? This has a straightforward solution if the denoiser can be expressed as a proximal map, as was shown to be the case for a class of linear symmetric denoisers. However, this result excludes kernel denoisers such as nonlocal means that are inherently non-symmetric. In this paper, we prove that a broader class of linear denoisers (including symmetric denoisers and kernel denoisers) can be expressed as a proximal map of some convex regularizer g. An algorithmic implication of this result for non-symmetric denoisers is that it necessitates appropriate modifications in the PnP updates to ensure convergence to a minimum of f+g. Apart from the convergence guarantee, the modified PnP algorithms are shown to produce good restorations.

Fixed-Point and Objective Convergence of Plug-and-Play Algorithms

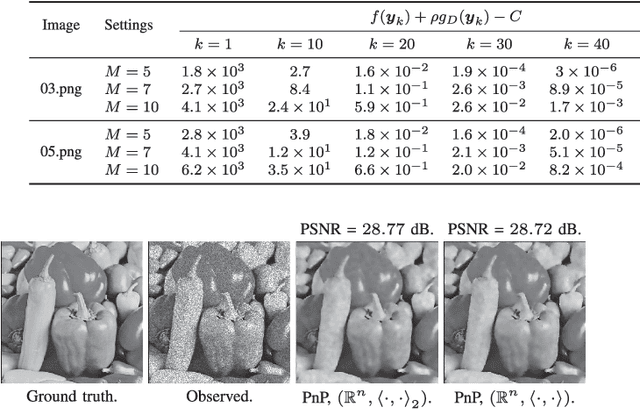
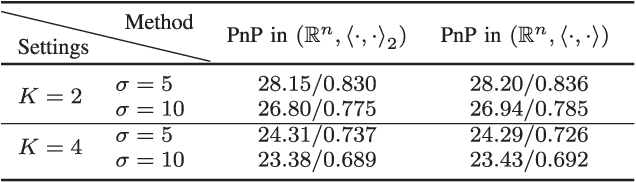
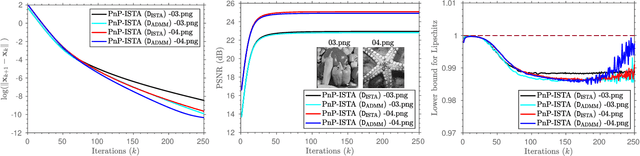
A standard model for image reconstruction involves the minimization of a data-fidelity term along with a regularizer, where the optimization is performed using proximal algorithms such as ISTA and ADMM. In plug-and-play (PnP) regularization, the proximal operator (associated with the regularizer) in ISTA and ADMM is replaced by a powerful image denoiser. Although PnP regularization works surprisingly well in practice, its theoretical convergence -- whether convergence of the PnP iterates is guaranteed and if they minimize some objective function -- is not completely understood even for simple linear denoisers such as nonlocal means. In particular, while there are works where either iterate or objective convergence is established separately, a simultaneous guarantee on iterate and objective convergence is not available for any denoiser to our knowledge. In this paper, we establish both forms of convergence for a special class of linear denoisers. Notably, unlike existing works where the focus is on symmetric denoisers, our analysis covers non-symmetric denoisers such as nonlocal means and almost any convex data-fidelity. The novelty in this regard is that we make use of the convergence theory of averaged operators and we work with a special inner product (and norm) derived from the linear denoiser; the latter requires us to appropriately define the gradient and proximal operators associated with the data-fidelity term. We validate our convergence results using image reconstruction experiments.

Plug-and-play ISTA converges with kernel denoisers

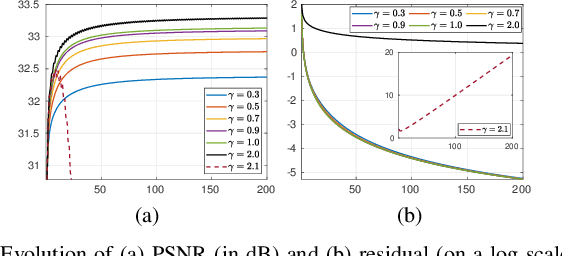
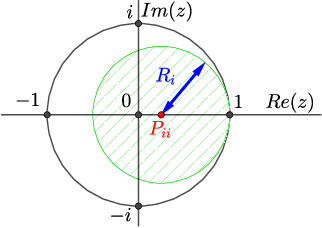
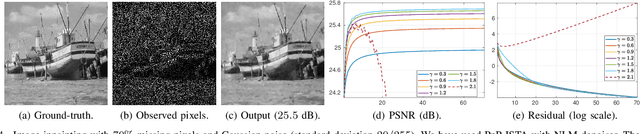
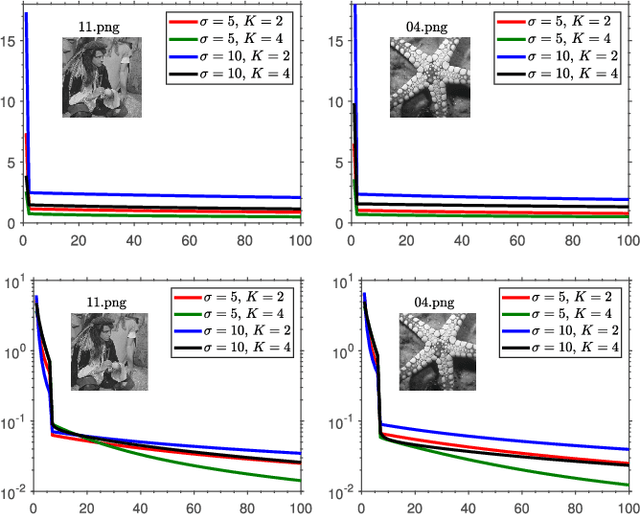
Plug-and-play (PnP) method is a recent paradigm for image regularization, where the proximal operator (associated with some given regularizer) in an iterative algorithm is replaced with a powerful denoiser. Algorithmically, this involves repeated inversion (of the forward model) and denoising until convergence. Remarkably, PnP regularization produces promising results for several restoration applications. However, a fundamental question in this regard is the theoretical convergence of the PnP iterations, since the algorithm is not strictly derived from an optimization framework. This question has been investigated in recent works, but there are still many unresolved problems. For example, it is not known if convergence can be guaranteed if we use generic kernel denoisers (e.g. nonlocal means) within the ISTA framework (PnP-ISTA). We prove that, under reasonable assumptions, fixed-point convergence of PnP-ISTA is indeed guaranteed for linear inverse problems such as deblurring, inpainting and superresolution (the assumptions are verifiable for inpainting). We compare our theoretical findings with existing results, validate them numerically, and explain their practical relevance.

On the Proof of Fixed-Point Convergence for Plug-and-Play ADMM

In most state-of-the-art image restoration methods, the sum of a data-fidelity and a regularization term is optimized using an iterative algorithm such as ADMM (alternating direction method of multipliers). In recent years, the possibility of using denoisers for regularization has been explored in several works. A popular approach is to formally replace the proximal operator within the ADMM framework with some powerful denoiser. However, since most state-of-the-art denoisers cannot be posed as a proximal operator, one cannot guarantee the convergence of these so-called plug-and-play (PnP) algorithms. In fact, the theoretical convergence of PnP algorithms is an active research topic. In this letter, we consider the result of Chan et al. (IEEE TCI, 2017), where fixed-point convergence of an ADMM-based PnP algorithm was established for a class of denoisers. We argue that the original proof is incomplete, since convergence is not analyzed for one of the three possible cases outlined in the paper. Moreover, we explain why the argument for the other cases does not apply in this case. We give a different analysis to fill this gap, which firmly establishes the original convergence theorem.