On the Construction of Averaged Deep Denoisers for Image Regularization
Paper and Code
Jul 15, 2022
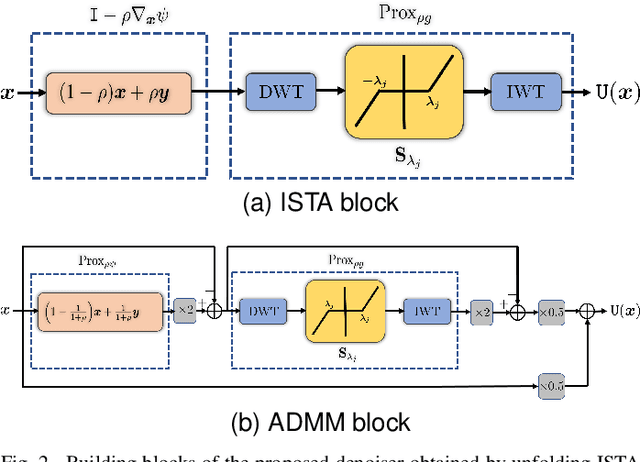
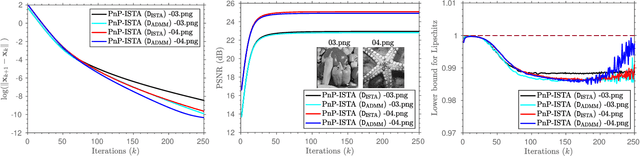

Plug-and-Play (PnP) and Regularization by Denoising (RED) are recent paradigms for image reconstruction that can leverage the power of modern denoisers for image regularization. In particular, these algorithms have been shown to deliver state-of-the-art reconstructions using CNN denoisers. Since the regularization is performed in an ad-hoc manner in PnP and RED, understanding their convergence has been an active research area. Recently, it was observed in many works that iterate convergence of PnP and RED can be guaranteed if the denoiser is averaged or nonexpansive. However, integrating nonexpansivity with gradient-based learning is a challenging task -- checking nonexpansivity is known to be computationally intractable. Using numerical examples, we show that existing CNN denoisers violate the nonexpansive property and can cause the PnP iterations to diverge. In fact, algorithms for training nonexpansive denoisers either cannot guarantee nonexpansivity of the final denoiser or are computationally intensive. In this work, we propose to construct averaged (contractive) image denoisers by unfolding ISTA and ADMM iterations applied to wavelet denoising and demonstrate that their regularization capacity for PnP and RED can be matched with CNN denoisers. To the best of our knowledge, this is the first work to propose a simple framework for training provably averaged (contractive) denoisers using unfolding networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge