Guided Nonlocal Patch Regularization and Efficient Filtering-Based Inversion for Multiband Fusion

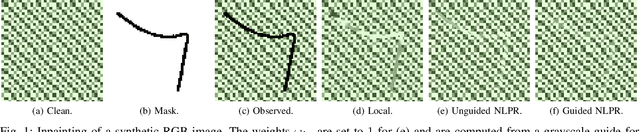
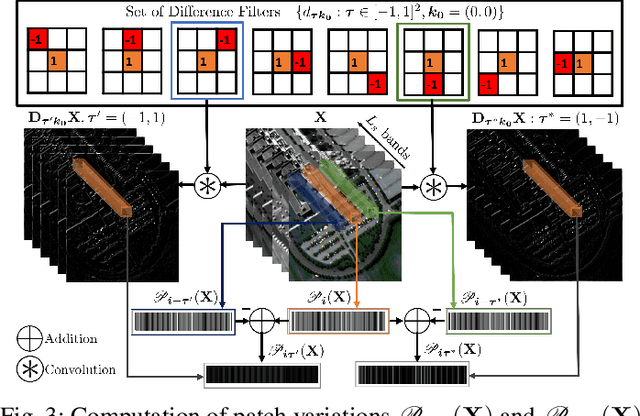
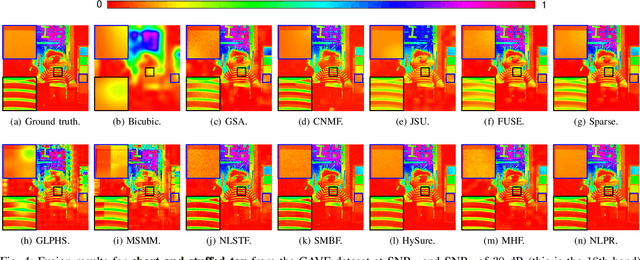
In multiband fusion, an image with a high spatial and low spectral resolution is combined with an image with a low spatial but high spectral resolution to produce a single multiband image having high spatial and spectral resolutions. This comes up in remote sensing applications such as pansharpening~(MS+PAN), hyperspectral sharpening~(HS+PAN), and HS-MS fusion~(HS+MS). Remote sensing images are textured and have repetitive structures. Motivated by nonlocal patch-based methods for image restoration, we propose a convex regularizer that (i) takes into account long-distance correlations, (ii) penalizes patch variation, which is more effective than pixel variation for capturing texture information, and (iii) uses the higher spatial resolution image as a guide image for weight computation. We come up with an efficient ADMM algorithm for optimizing the regularizer along with a standard least-squares loss function derived from the imaging model. The novelty of our algorithm is that by expressing patch variation as filtering operations and by judiciously splitting the original variables and introducing latent variables, we are able to solve the ADMM subproblems efficiently using FFT-based convolution and soft-thresholding. As far as the reconstruction quality is concerned, our method is shown to outperform state-of-the-art variational and deep learning techniques.

Plug-and-Play Regularization using Linear Solvers

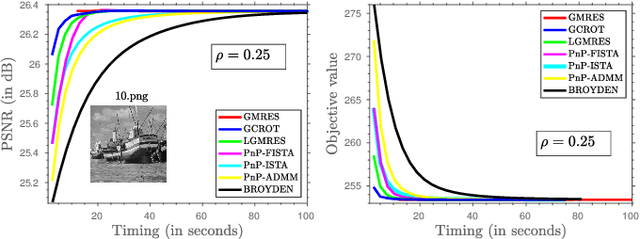
There has been tremendous research on the design of image regularizers over the years, from simple Tikhonov and Laplacian to sophisticated sparsity and CNN-based regularizers. Coupled with a model-based loss function, these are typically used for image reconstruction within an optimization framework. The technical challenge is to develop a regularizer that can accurately model realistic images and be optimized efficiently along with the loss function. Motivated by the recent plug-and-play paradigm for image regularization, we construct a quadratic regularizer whose reconstruction capability is competitive with state-of-the-art regularizers. The novelty of the regularizer is that, unlike classical regularizers, the quadratic objective function is derived from the observed data. Since the regularizer is quadratic, we can reduce the optimization to solving a linear system for applications such as superresolution, deblurring, inpainting, etc. In particular, we show that using iterative Krylov solvers, we can converge to the solution in a few iterations, where each iteration requires an application of the forward operator and a linear denoiser. The surprising finding is that we can get close to deep learning methods in terms of reconstruction quality. To the best of our knowledge, the possibility of achieving near state-of-the-art performance using a linear solver is novel.

On the Construction of Averaged Deep Denoisers for Image Regularization

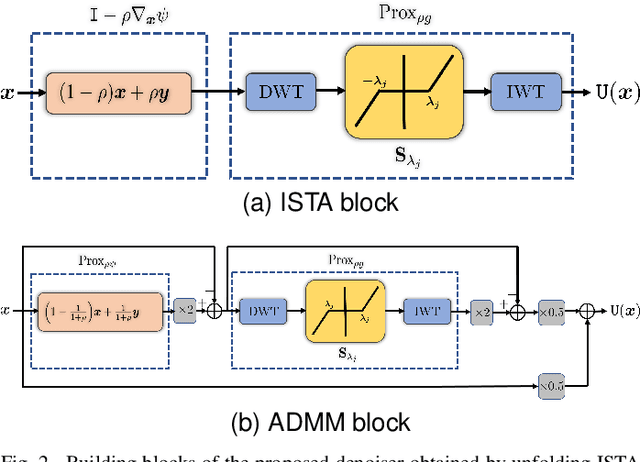
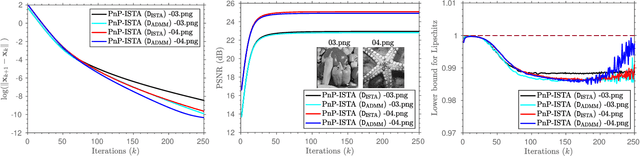
Plug-and-Play (PnP) and Regularization by Denoising (RED) are recent paradigms for image reconstruction that can leverage the power of modern denoisers for image regularization. In particular, these algorithms have been shown to deliver state-of-the-art reconstructions using CNN denoisers. Since the regularization is performed in an ad-hoc manner in PnP and RED, understanding their convergence has been an active research area. Recently, it was observed in many works that iterate convergence of PnP and RED can be guaranteed if the denoiser is averaged or nonexpansive. However, integrating nonexpansivity with gradient-based learning is a challenging task -- checking nonexpansivity is known to be computationally intractable. Using numerical examples, we show that existing CNN denoisers violate the nonexpansive property and can cause the PnP iterations to diverge. In fact, algorithms for training nonexpansive denoisers either cannot guarantee nonexpansivity of the final denoiser or are computationally intensive. In this work, we propose to construct averaged (contractive) image denoisers by unfolding ISTA and ADMM iterations applied to wavelet denoising and demonstrate that their regularization capacity for PnP and RED can be matched with CNN denoisers. To the best of our knowledge, this is the first work to propose a simple framework for training provably averaged (contractive) denoisers using unfolding networks.

Fixed-Point and Objective Convergence of Plug-and-Play Algorithms

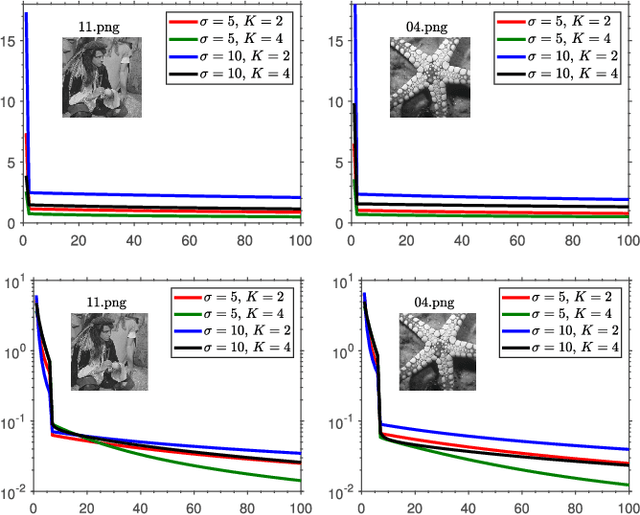
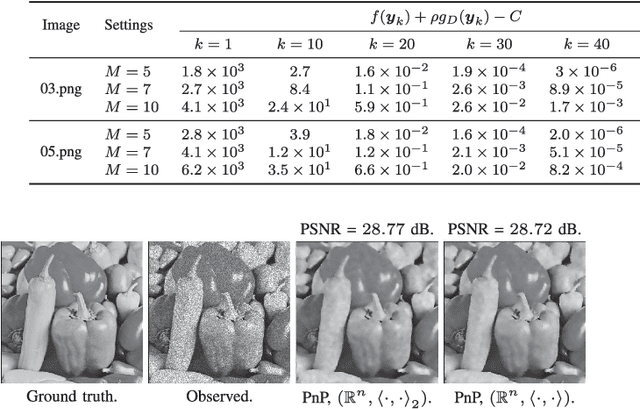
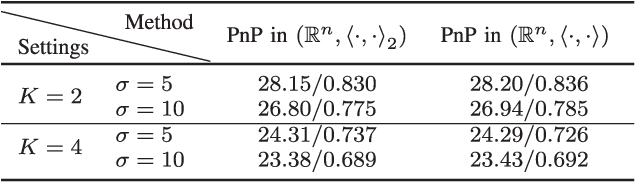
A standard model for image reconstruction involves the minimization of a data-fidelity term along with a regularizer, where the optimization is performed using proximal algorithms such as ISTA and ADMM. In plug-and-play (PnP) regularization, the proximal operator (associated with the regularizer) in ISTA and ADMM is replaced by a powerful image denoiser. Although PnP regularization works surprisingly well in practice, its theoretical convergence -- whether convergence of the PnP iterates is guaranteed and if they minimize some objective function -- is not completely understood even for simple linear denoisers such as nonlocal means. In particular, while there are works where either iterate or objective convergence is established separately, a simultaneous guarantee on iterate and objective convergence is not available for any denoiser to our knowledge. In this paper, we establish both forms of convergence for a special class of linear denoisers. Notably, unlike existing works where the focus is on symmetric denoisers, our analysis covers non-symmetric denoisers such as nonlocal means and almost any convex data-fidelity. The novelty in this regard is that we make use of the convergence theory of averaged operators and we work with a special inner product (and norm) derived from the linear denoiser; the latter requires us to appropriately define the gradient and proximal operators associated with the data-fidelity term. We validate our convergence results using image reconstruction experiments.

Fast High-Dimensional Kernel Filtering

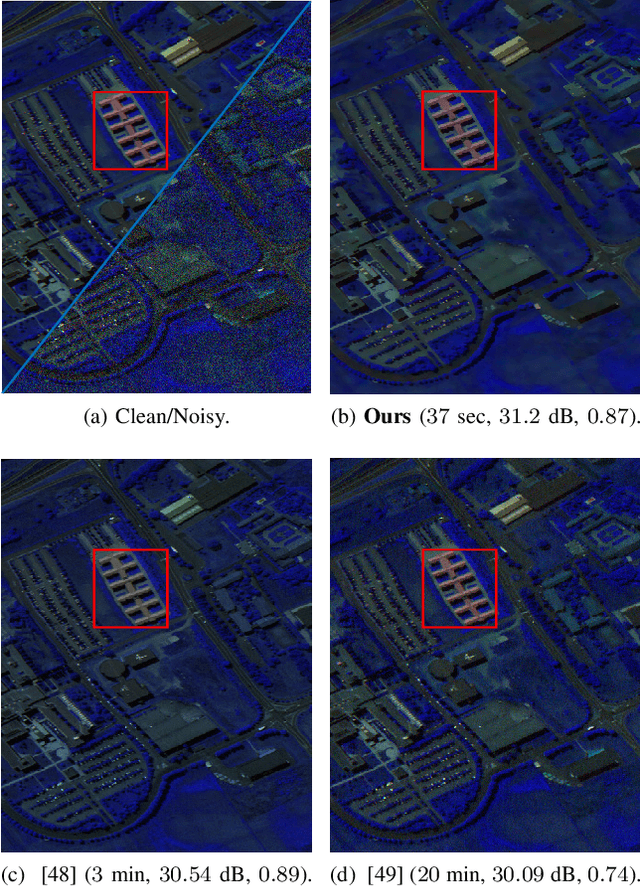
The bilateral and nonlocal means filters are instances of kernel-based filters that are popularly used in image processing. It was recently shown that fast and accurate bilateral filtering of grayscale images can be performed using a low-rank approximation of the kernel matrix. More specifically, based on the eigendecomposition of the kernel matrix, the overall filtering was approximated using spatial convolutions, for which efficient algorithms are available. Unfortunately, this technique cannot be scaled to high-dimensional data such as color and hyperspectral images. This is simply because one needs to compute/store a large matrix and perform its eigendecomposition in this case. We show how this problem can be solved using the Nystr\"om method, which is generally used for approximating the eigendecomposition of large matrices. The resulting algorithm can also be used for nonlocal means filtering. We demonstrate the effectiveness of our proposal for bilateral and nonlocal means filtering of color and hyperspectral images. In particular, our method is shown to be competitive with state-of-the-art fast algorithms, and moreover it comes with a theoretical guarantee on the approximation error.

Fast High-Dimensional Bilateral and Nonlocal Means Filtering

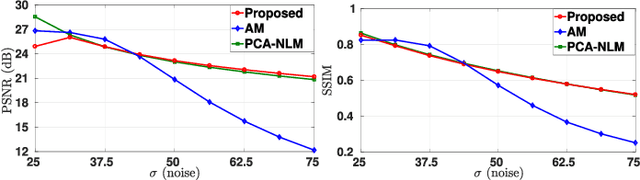
Existing fast algorithms for bilateral and nonlocal means filtering mostly work with grayscale images. They cannot easily be extended to high-dimensional data such as color and hyperspectral images, patch-based data, flow-fields, etc. In this paper, we propose a fast algorithm for high-dimensional bilateral and nonlocal means filtering. Unlike existing approaches, where the focus is on approximating the data (using quantization) or the filter kernel (via analytic expansions), we locally approximate the kernel using weighted and shifted copies of a Gaussian, where the weights and shifts are inferred from the data. The algorithm emerging from the proposed approximation essentially involves clustering and fast convolutions, and is easy to implement. Moreover, a variant of our algorithm comes with a guarantee (bound) on the approximation error, which is not enjoyed by existing algorithms. We present some results for high-dimensional bilateral and nonlocal means filtering to demonstrate the speed and accuracy of our proposal. Moreover, we also show that our algorithm can outperform state-of-the-art fast approximations in terms of accuracy and timing.